library(sde) (R)
Rのパッケージ,library(sde)の紹介です.
このパッケージでは確率過程のシミュレーションが簡単にできます.
たとえばブラウン運動を発生させたければ
> BM function (x = 0, t0 = 0, T = 1, N = 100)
という関数を使うことで,
初期値$x$,初期時刻$t_0$,最終時刻$T$,シミュレーション刻み幅$(T-t_0)/N$
のブラウン運動のパスが生成できます.
この関数を使って
BMpath <- BM(x = 0, t0 = 0, T = 1, N = 1000) plot(BMpath)
とすれば,下のようなブラウン運動が生成できます.

このほかにも,ブラウン橋
BBridge(x=0, y=0, t0=0, T=1, N=100)
や確率微分方程式の解
sde.sim(t0 = 0, T = 1, X0 = 1, N = 100, delta, drift, sigma, drift.x, sigma.x, drift.xx, sigma.xx, drift.t, method = c("euler", "milstein", "KPS", "milstein2", "cdist","ozaki","shoji","EA"), alpha = 0.5, eta = 0.5, pred.corr = T, rcdist = NULL, theta = NULL, model = c("CIR", "VAS", "OU", "BS"), k1, k2, phi, max.psi = 1000, rh, A, M=1)
のシミュレーションなども簡単にでき,便利です.
最後に$B_t$を0を出発する標準ブラウン運動として
\[
\mathrm{E} \bigg[B_t\int_0^t B_s {\rm d}s \bigg],
\]
の値をモンテカルロ法で計算したいと思います.
ちなみに解析解は,まず伊藤の公式から
\[
\int_0^t B_s {\rm d}s=tB_t-\int_0^t s {\rm d}B_s,
\]
なので
\begin{eqnarray*}
\mathrm{E} \bigg[B_t\int_0^t B_s {\rm d}s \bigg]&=&t\mathrm{E}[B_t^2]-E[B_t\int_0^t s {\rm d}B_s]\\
&=&t^2-\mathrm{E}\langle B_t, \int_0^t s {\rm d}B_s\rangle\\
&=&t^2-\mathrm{E}\int_0^t s {\rm d}s\\
&=&\frac{t^2}{2}.
\end{eqnarray*}
Rのコードは下の通り.
#E[B_t \int_0^t B_s ds]の計算(モンテカルロ法) library(sde) time_max <- 10 #[0,time_max]までBMをシミュレーション sim_num <- 1000 #BMの各時刻での発生回数 crossvar_mean <- rep(NaN, time_max) crossvar <- rep(NaN, sim_num) for(i in 1:time_max){ for(j in 1:sim_num){ #BMのpathを生成 BMpath <- BM(T=i, N=100*i) #\int_0^t B_s ds (リーマン和) int_Bs_ds <- sum(BMpath[1:(100*i)]/100) crossvar[j] <- BMpath[100*i+1]*int_Bs_ds } crossvar_mean[i] <- mean(crossvar) } plot(crossvar_mean)
結果は以下の通り.

解析解と一致していることが分かります.
主成分分析(R)
PRML(12章)のまとめです.
観測値 $\{x_n\}_{n=1}^N\subset \mathbf{R}^D$ があるとき,$u_1\in\mathbf{R}^D$への観測値の射影が最大になるような $u_1\in\mathbf{R}^D$ を探すことを考えます.
$u_1$ は観測値 $\{x_n\}_{n=1}^N$ の一番の【特徴】を表す方向であると考えられます.極端な例でいうと,$u_1$ 方向に射影したとき観測値がすべて一点に集約されてしまっては,観測値の持っている情報は無くなってしまうと考えられます.そこで射影したときに射影した観測値の分散が最大になる方向は,射影したときの観測値の情報を最大限保持する方向であると考えられます.
$u_1$だけでなく,$u_2,\ldots, u_M$まで同様に考えて,$D$次元の観測値$\{x_n\}_{n=1}^N\subset \mathbf{R}^D$を$M$次元の$u_1,\ldots,u_M$の張る空間への射影を考えたのが主成分分析になります.
高次元データを$2$次元に射影して可視化するときや,データの圧縮,データの白色化に使われます.
Rによる例
主成分分析はRの関数prcomp()を使うことでできます.以下ではFisherのあやめのデータ(iris)で主成分分析した結果を載せてあります.主部分空間(2次元)で見たときに種によって結構分かれている気がします.
#iris data #pca(prcomp) data(iris) iris.data <- iris[, 1:4] iris.lab <- iris[, 5] result.pca <- prcomp(data.matrix(iris.data), scale = TRUE) #label lab <- as.integer(iris.lab) lev <- levels(iris.lab) #plot plot(result.pca$x[, 1:2], col=lab, pch=lab) par(new = TRUE) legend("topright", legend = lev, col = 1:3, pch = 1:3)

ちなみに第3, 4主成分(寄与率の最も低い二つの主成分)に関して描画すると以下のようになります:

定性的な理解通り,寄与率の低い方向に関して描画しても,あまり元のデータの特徴は捉えられていないかと思います.
分散最大化による定式化
具体的に $u_1$ を求める方法は以下のようになります:
(射影されたデータの分散)$=\frac{1}{N}\sum_{n=1}^N(u_1^{\top}(x_n-\bar{x}))$
これを $u_1^{\top}u_1=1$ の制約条件(方向だけに興味があるので規格化の制約をつけます)のもとで解くと(ラグランジュの未定乗数法)
\[
u_1=共分散行列の最大固有値に対応する固有ベクトル
\]
となります.上位$M$個の固有ベクトルを考えれば $u_1,u_2,\ldots,u_M$ に相当します.射影誤差の最小化としても $u_1,\ldots,u_M$ が得られます.射影誤差の最小化はデータの近似(データ圧縮)の考え方に基づきます.
確率的主成分分析(最尤推定量としての解釈)
上で述べた主成分分析の結果は,ある確率モデルの最尤推定量として表現することができます.最尤推定量として表現できること自体も面白い性質ですが,この表現により主成分分析のベイズ的扱いが可能になるという実際的な利点もあります.
主成分分析は次のような確率モデルの最尤推定量として得ることができます:
$z$を潜在変数とします.$z$ は$M$次元の標準正規分布 $\mathcal{N}(z|0, I)$ に従うとします:
\[
p(z)=\mathcal{N}(z|0, I)
\]
$D\times M$ 行列 $W$ と $\mu, \sigma^2$ をパラメータとして,$z$ が与えられた下での $x$ の確率分布を
\[
p(x|z)=\mathcal{N}(x|Wz+\mu, \sigma^2I)
\]
とします.この確率モデルのパラメータ $W$ の最尤推定量 $\hat{W}$ の$M$本の列ベクトルが主成分分析で得られる$u_1,\ldots, u_M$に一致します.
この確率モデルの解釈は次のようになると思います:
$\mu$は観測値$\{x_n\}_{n=1}^N$の平均$\bar{x}$で,$z$は$\mu$からの "$M$" 次元空間内でのデータの分布を表します.$W$はデータの分布している潜在的な低次元の線形空間(多様体)から$D$次元への写像を表します($M$次元空間の標準基底の行先($D$次元空間の直交系)を選べば写像が決まります).$z$は重要で,ただの潜在変数というだけでなく,観測データの中には低次元($M$次元)の自由度しかないという気持ちを表したものであると考えられます.
潜在変数を導入した確率モデルを考えることで,EMアルゴリズムを使って主成分分析を行うことができます.これはデータの次元$D$が非常に大きく,固有ベクトルを求めることが計算的に厳しい時に役に立ちます(確率的解釈をしたことで得られる利点の一つです).
ベイズ的主成分分析
上にも述べたように主成分分析の確率的解釈のおかげでベイズ推定を行うことができます.ベイズ的に考えることの利点の一つに関連自動決定ということがあげられます.上で述べた主成分分析では,主部分空間 $W$ の次元 $M$ を固定していましたが,データの可視化($M=2$)などの場合以外は$M$をどう決めればよいかは不明です.ベイズでは事前分布を決めることで自動的に"枝刈り"して次元 $M$ を調節します(モデルの複雑度とデータへの当てはまりの良さのトレードオフ).とPRMLには説明がありますが,これも事前分布の入れ方によって変わるのかなと思います.つまり自分で主部分空間の次元を決める代わりに,事前分布を決める必要が出てくると思います.
カーネル主成分分析
観測データの主成分を見るのではなく,一回特徴ベクトルでデータを変換してから主成分分析を行う方法がカーネル主成分分析になります.
こうすることで,非線形の部分空間(多様体)に射影することができます.この特徴ベクトルを陽に指定しなくても,内積の形だけがわかれば特徴ベクトルで変換した方で主成分分析ができます(カーネルトリック).

実際にRでカーネル主成分分析をやってみます.
ガウシアンカーネルでカーネルのパラメータsigmaを0.0003にした場合です.同様にsigmaを0.1, 1, 10, 100に変えて主成分分析した結果です.
#package 'kernlab' = kernel pca library(kernlab) data(iris) iris.data <- iris[, 1:4] iris.lab <- iris[, 5] #label lab <- as.integer(iris.lab) lev <- levels(iris.lab) #kernel pca #kernel = gaussian, sigma=0.0003 #feature dim =2 result <- kpca(~., data=iris.data, features=2, kpar=list(sigma=0.0003)) plot(rotated(result), col=lab, pch=lab) #legend legend("topright", legend=lev, pch=1:3, col=1:3)





sigmaによって結果が大きく違うことがわかります.
multicore (R)
Rのライブラリ multicore を試した結果です.
mclappy()という関数を使いました.
この関数は lapply() を並列でできるようにしたもので,
独立に繰り返し計算する必要がある場合(乱数や初期値を変えた結果が欲しいときなど)
に簡単に並列で計算できます.
例えば k-means 法を R で行う場合に kmeans() という関数があります.
この関数は
kmeans(x, centers, iter.max = 10, nstart = 1, algorithm = c("Hartigan-Wong", "Lloyd", "Forgy", "MacQueen"))
という形になっていて,x としてクラスタリングしたいデータ,centers に
クラスタ数をとります.このときクラスターの初期値を nstart 回ランダムに選び,
その結果もっともクラスター内平方和(tot.withinss)を小さくした結果を返します.
k-meansの各初期値からの反復は,ほかの初期値を選んだ場合の結果に依存しないので
簡単に並列化できると考えられます.
そこで並列で計算させた場合にどれくらい早くなるか実験しました.
まず mclapply() は
mclapply(X, FUN, ..., mc.preschedule = TRUE, mc.set.seed = TRUE, mc.silent = FALSE, mc.cores = 1L, mc.cleanup = TRUE, mc.allow.recursive = TRUE)
となっています.
lapply() と同じで,X の要素に関数 FUN を作用させた結果をリストで返します.
mc.cores が(最大限)使うコアの数です.
これを踏まえ,ライブラリMASSにあるデータ Boston を4つのクラスタに k-means 法を使ってクラスタリングしました.
初期値は 5000*n 個 (n=1,2,...,10) 与え,並列したときとかかった時間の差を調べました.
並列させないときは
t <- proc.time() invisible(kmeans(Boston, 4, nstart=5000*n)) duration <- (proc.time() - t)[3]
で時間を計り,並列させたときは
t <- proc.time() results <- mclapply(rep(5000*n/8, 8), function(nstart) kmeans(Boston, 4, nstart=nstart)) #collect results objective.values <- sapply(results, function(result) result$tot.withinss) result.best <- results[[which.min(objective.values)]] duration <- (proc.time() - t)[3]
で時間を計りました.
#collect results の後の二行はクラスター内平方和(tot.withinss)を小さくした結果を返すための部分です.
mclapply() は mc.cores を指定しないと,自動で使えるコアの数を調べます.
自分が実験した環境だとコアの数が8だったので,5000*n個の初期値を
8個に分割しています.分割数に差があるかどうかを調べるために
9個に分割した場合も調べました:
t <- proc.time() results <- mclapply(rep(5000*n/9, 9), function(nstart) kmeans(Boston, 4, nstart=nstart)) objective.values <- sapply(results, function(result) result$tot.withinss) result.best <- results[[which.min(objective.values)]] duration <- (proc.time() - t)[3]
細かいですが kmeans() は nstart の値が小数でもエラーがでず,nstartの小数以下を切り捨てた回数だけ初期値をランダムに発生させて計算しています(1:4.5と1:4が同じため).
結果としては次のようになりました:

横軸は初期値の数(5000*n),縦軸はかかった時間です.
凡例の cores の値は使ったコアの数で,list の値は 5000*n 個の初期値の分割数です.
コア数が多い方が当然早く計算ができることが分かりました.
また初期値の分割数はコア数の倍数にした方がいいと思われます.
実際 multicore のマニュアルを読むと
"By default (mc.preschedule=TRUE) the input vector/list X is split into as many parts as there are cores (currently the values are spread across the cores sequentially, i.e. first value to core 1, second to core 2, ... (core + 1)-th value to core 1 etc.) and then one process is spawned to each core and the results are collected."
とあります.そこでコア数の倍数である16, 24分割した場合は8分割の場合とほとんど同じ結果になりました(凡例の一番上はcores=8の間違いです):

以上をまとめると
・並列計算したほうが早く,multicoreのmclapply()で簡単にできる
・初期値や乱数の分割はコア数の倍数にした方が良い(一つ一つの計算量が同じなら)
snowとかも調べてみたいと思います.
Contiguity
統計にでてくるContiguityの概念についての問題(van der Vaart: Asymptotic Statistics. Chap 6.)を解いたので,そのまとめです.
問題
(1) 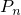 を標準正規分布,
を標準正規分布,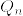 を平均
を平均 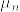 分散1の正規分布とする.このとき
分散1の正規分布とする.このとき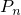 と
と 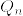 が互いにcontiguousであることと,
が互いにcontiguousであることと,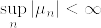 は同値であることを示せ.
は同値であることを示せ.
(2) total variation を
とすると
(3) 任意の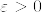 に対して,
に対して,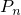 と
と 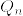 は互いにcontiguousであるが,
は互いにcontiguousであるが,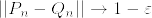 となる例を見つけよ.
となる例を見つけよ.
(4) 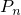 は
は 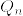 に対してcontiguousであるが,
に対してcontiguousであるが,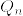 は
は 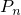 に対してcontiguousでない例を挙げよ.
に対してcontiguousでない例を挙げよ.
(5) 二つの確率測度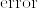 ,
, 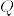 が互いに絶対連続であることと,確率測度の列
が互いに絶対連続であることと,確率測度の列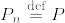 ,
, 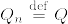 が互いにcontiguousであることは同値である.
が互いにcontiguousであることは同値である.
証明
(1) 互いにcontiguousなら,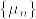 が有界であることを対偶を使って示す.
が有界であることを対偶を使って示す.
とする.このとき 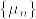 の部分列で
の部分列で 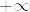 または
または 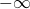 となるものが存在する.この部分列を
となるものが存在する.この部分列を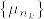 とし,
とし,
とすると,
より互いにcontiguousでない.よって互いにcontiguousなら,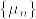 が有界である.
が有界である.
逆を示す.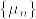 が有界であるとする.
が有界であるとする.%3D0.png) とする.
とする.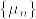 が有界であるから,任意の
が有界であるから,任意の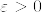 に対して,ある
に対して,ある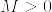 があって,
があって,
となる(tight).このとき
となるから,
よって 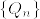 は
は 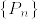 に対してcontiguous.同様に
に対してcontiguous.同様に 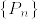 は
は 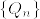 に対してcontiguousであることが分かる.よって同値性が示された.
に対してcontiguousであることが分かる.よって同値性が示された.
(2) %3D0.png) とする.total variationが0に収束するという仮定より,任意の
とする.total variationが0に収束するという仮定より,任意の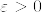 に対して,ある
に対して,ある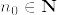 があって,
があって,
よって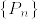 は
は 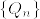 に対してcontiguousであることが示された.条件の対称性から同様にして,互いにcontiguousであることが分かる.
に対してcontiguousであることが示された.条件の対称性から同様にして,互いにcontiguousであることが分かる.
(3) 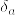 を
を 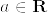 に台を持つディラック測度とする.
に台を持つディラック測度とする.
とすれば互いにcontiguousであるが,total variation は集合{0}のときに となる.
となる.
(4)
とすれば条件を満たす.
(5) 二つの確率測度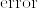 ,
, 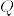 が互いに絶対連続であるとする.このときラドン--ニコディム微分
が互いに絶対連続であるとする.このときラドン--ニコディム微分
はそれぞれの確率測度の下で可積分である.
であるから,
よって 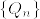 は
は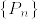 に対してcontiguousである.全く同様にして
に対してcontiguousである.全く同様にして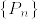 は
は 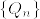 に対してcontiguousである.
に対してcontiguousである.
次に確率測度の列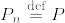 ,
, 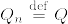 が互いにcontiguousであるとする.
が互いにcontiguousであるとする.%3D0.png) とする.
とする.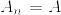 とすれば,contiguityより
とすれば,contiguityより%3DQ(A)%3D0.png) .よってQはPに関して絶対連続.同様にPはQに関して絶対連続.[証明終]
.よってQはPに関して絶対連続.同様にPはQに関して絶対連続.[証明終]
Ostrowski-Taussky Inequality
Ostrowski-Taussky Inequality
Aを正方行列とし,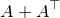 が正定値行列であるとする.このとき以下の不等式が成立する:
が正定値行列であるとする.このとき以下の不等式が成立する:
となっている.このような行列に関して次の不等式が成立する(下の補第参照):
これが成り立てば
これより証明が終わる.あとは次の補題1を示せばよい.ただし帰納法の成立のため主張を拡張する.
補第1
証明
Bの次元に関する帰納法で示す.n=1のときは明らかに成立する.n=k-1のとき成立するとする.まず次のように行列Bを分割する.
ここでCは(k-1)×(k-1)行列である.まず任意の%5E%7B%5Ctop%7D%5Cin%5Cmathbf%7BR%7D%5En.png) に対して,
に対して,%5E%7B%5Ctop%7D.png) として,
として,
となることがまずわかる.
次に, よりブロック行列の行列式を考えれば
よりブロック行列の行列式を考えれば
帰納法の仮定からCは正則であるから,Sherman-Morrison-Woodburyの公式より
ここで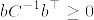 であることがわかる.実際帰納法の仮定より
であることがわかる.実際帰納法の仮定より
Cは正則だから任意のxに対してあるyがあって
よって任意のxに対して
となるためである.これより
[証明終]
主張が言いたいことを考えると,これは複素数zに対する不等式
の行列への拡張ではないかという指摘を受けました.というのも
と分けます.右辺の第一項はAを対称化したもので,第二項は反対称化したものです.実対称行列の固有値は実数で,反対称行列の固有値は純虚数です.つまり固有値の視点から見ると,上の分解は行列の実部と虚部への分解に対応するものではないかと考えられます.そうすると主張の左辺はAの固有値の実部の積,右辺は固有値の絶対値の積なので,不等号が成り立つと思われます.これを正当化するには,右辺の第一項と第二項が同時三角化可能で,行列の和の固有値が,各行列の固有値の和になることを言わないとダメだと思いますが...
ちなみに主張の右辺の絶対値は要らないことが証明から分かります.
ゼータ分布に従う独立な確率変数が互いに素になる確率[D.Williams]
主張
X,Yは独立にゼータ分布に従うものとする.つまり
とする.このとき
(gcdは最大公約数)とすると,
となる.[D.Williams: Probability with martingales, p226]
証明
であるため.これより
となる.
次に.png) つまりX,Yが互いに疎になる確率を計算する.
つまりX,Yが互いに疎になる確率を計算する.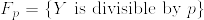 ,
,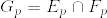 とすれば
とすれば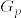 達は独立である.実際
達は独立である.実際
よりわかる.従って
\begin{eqnarray*}
P(H=1)
&=&P\bigg(\bigcap_{p:{\rm prime}}(E_p\cap F_p)^c\bigg)\\
&=&\prod_{p:{\rm prime}} P((E_p\cap F_p)^c)\\
&=&\prod_{p:{\rm prime}} (1-1/p^{2s})\\
&=&\frac{1}{\zeta(2s)}
\end{eqnarray*}
Xがpの倍数であるときのXの分布は,またゼータ分布になる:
nが素数でないときも
と定義すれば,条件付き期待値の性質から
となって示された.(包除原理を使って計算する方が正確だと思われます)[証明終]
ちなみにgcd(X,Y)の可測性は
から分かります.また結局互いに素な確率は
ということもわかり,面白いと思いました.
Hilbert--Schmidt作用素はコンパクト作用素
主張
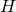 を可分なヒルベルト空間とし,
を可分なヒルベルト空間とし,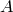 を
を 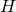 から
から 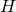 へのHilbert-Schmidt作用素とする.このとき
へのHilbert-Schmidt作用素とする.このとき 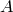 はコンパクト作用素である.
はコンパクト作用素である.
証明
事実1
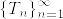 をコンパクト作用素とし,
をコンパクト作用素とし,
であるならば, 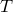 はコンパクトである(コンパクト作用素の全体はバナッハ空間なので).
はコンパクトである(コンパクト作用素の全体はバナッハ空間なので).
事実2
有界線形作用素の値域が有限次元空間であればコンパクトである(有限次元と局所コンパクトは同値).
この二つの事実を用います.
 を
を 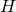 の内積とし,
の内積とし,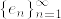 を完全正規直交系とする.有界線形作用素
を完全正規直交系とする.有界線形作用素 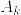 を
を
と定義する.事実2より 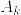 はコンパクト.
はコンパクト. 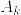 が
が 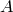 に強収束することを示せば,事実1より
に強収束することを示せば,事実1より 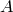 はコンパクトとなり,主張が示されたことになる.
はコンパクトとなり,主張が示されたことになる.
となる.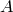 はHilbert-Schmidt作用素であるから,
はHilbert-Schmidt作用素であるから,
Hui-Hsiung Kuoの Gaussian Measures in Banach Spacesという本を読み始めました.上の主張はこの本のExerciseになっています.抽象ウィナー空間が分かるようになりたいです.
 | Gaussian Measures in Banach Spaces Hui-Hsiung Kuo 2006-06-29 売り上げランキング : 1234523 Amazonで詳しく見る by G-Tools |
-Q(A)%7C.png)
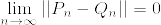
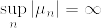
%5C%5C%0A(%5Cmu_%7Bn_k%7D,%5Cinfty)%20%20%26%20(n%3Dn_k,%20%5Cmu_%7Bn_k%7D%5Cgeq%200)%5C%5C%0A(n,%5Cinfty)%20%26%20(n%5Cneq%20n_k)%5C%5C%0A%5Cend%7Barray%7D%0A%5Cright..png)
%3D0,%5Cquad%20%5Climsup_%7Bn%7DQ_n(A_n)%5Cgeq%201/2.png)
%3C%5Cvarepsilon.png)
%26%3D%26%5Cint_%7B%5Cmathbf%7BR%7D%7D1_%7BA_n%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%7D%5Cexp%5Cbigg(-%5Cfrac%7B(x-%5Cmu_n)%5E2%7D%7B2%7D%5Cbigg)%7B%5Crm%20d%7Dx%5C%5C%0A%26%3D%26%5Cint_%7B%7Cx%7C%3EM%7D%20+%20%5Cint_%7B%7Cx%7C%5Cleq%20M%7D%5C%5C%0A%26%3C%20%26%5Cvarepsilon%20+%20%5Cint_%7B%7Cx%7C%5Cleq%20M%7D1_%7BA_n%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%7D%5Cexp%5Cbigg(-%5Cfrac%7Bx%5E2%7D%7B2%7D%5Cbigg)%5Cexp%5Cbigg(%5Cmu_n%20x-%5Cfrac%7B%5Cmu_n%5E2%7D%7B2%7D%5Cbigg)%7B%5Crm%20d%7Dx%5C%5C%0A%26%5Cleq%20%26%5Cvarepsilon%20+%20%5Cexp(CM)P_n(A_n)%5Cquad%20(C%3D%5Csup_n%7C%5Cmu_n%7C,%20%5Cexp(-%5Cmu_n%5E2/2)%5Cleq%201).png)
%5Cleq%20%5Cvarepsilon.png)
%3C%5Cvarepsilon/2..png)

%3D(P_n(A_n)-Q_n(A_n))+Q_n(A_n)%5Cleq%20%7C%7CP_n-Q_n%7C%7C+Q_n(A_n)%3C%5Cvarepsilon.png)
%5Cdelta_0+%5Cfrac%7B%5Cvarepsilon%7D%7B2%7D%5Cdelta_1.png)
%5Cdelta_1.png)
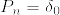
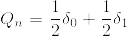
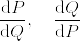
%3D0%5CRightarrow%20%5Clim_n%201_%7BA_n%7D%3D0%20%5Cquad%20P-%7B%5Crm%20a.s.%7D%0A.png)
%3D%5Cint%201_%7BA_n%7D%5Cfrac%7B%7B%5Crm%20d%7DQ%7D%7B%7B%5Crm%20d%7DP%7D%7B%5Crm%20d%7DP%5Cto%20%5Cint%200%5Ccdot%20%5Cfrac%7B%7B%5Crm%20d%7DQ%7D%7B%7B%5Crm%20d%7DP%7D%7B%5Crm%20d%7DP%3D0%5C%5C(%7B%5Crm%20Lebesgue's%20%5C%20convergence%5C%20%20theorem.%7D).png)
%5Cleq%20%7C%5Cdet(A)%7C..png)
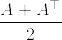
P%3D%7B%5Crm%20diag%7D[%5Clambda_1,%5Cldots,%5Clambda_n],%5Cquad%20%5Clambda_i%3E0~(i%3D1,2,%5Cldots,n).png)
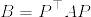
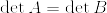
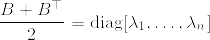
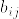
%5C%5C%0A-b_%7Bji%7D%20%26%20(i%5Cneq%20j)%0A%5Cend%7Barray%7D%0A%5Cright..png)
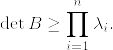
%26%3D%26%5Cdet(%7B%5Crm%20diag%7D[%5Clambda_1,%5Cldots,%5Clambda_n])%5C%5C%0A%26%3D%26%5Cprod_%7Bi%3D1%7D%5En%5Clambda_i%5C%5C%0A%26%5Cleq%20%26%5Cdet%20B%5C%5C%0A%26%3D%26%5Cdet%20A..png)
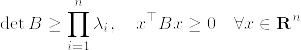
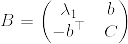
%5E2+(%5Chat%7Bx%7D%5E%7B%5Ctop%7DC%5Chat%7Bx%7D)%5Cgeq%200.png)
..png)
%3D%5Clambda_1(1+bC%5E%7B-1%7Db%5E%7B%5Ctop%7D)%5Cdet%20C%5C%5C%0A.png)
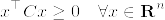
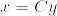
%5E%7B%5Ctop%7D%5C%5C%0A%26%3D%26y%5E%7B%5Ctop%7DCy%5Cgeq%200.png)
%5Cdet%20C%5C%5C%0A%26%5Cgeq%20%26%5Clambda_1%5Cdet%20C%5C%5C%0A%26%5Cgeq%20%26%5Cprod_%7Bi%3D1%7D%5En%5Clambda_i..png)
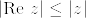
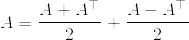
%3D%5Cfrac%7B1%7D%7Bn%5Es%5Czeta(s)%7D%20%5Cquad%20(%5Czeta(s):%3D%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7Bn%5Es%7D,s%3E1).png)
.png)
%3D%5Cfrac%7B1%7D%7Bn%5E%7B2s%7D%5Czeta(2s)%7D.png)
.png)
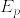
%26%3D%26%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7DP(X%3Dni_1%5Ccdots%20i_p)%5C%5C%0A%26%3D%26%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7B(ni_1%5Ccdots%20i_p)%5Es%5Czeta(s)%7D%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B(i_1%5Ccdots%20i_p)%5Es%7D.png)
%3D%5Cfrac%7B1%7D%7B(i_1%5Ccdots%20i_p)%5Es%7D.png)
%26%3D%26P(X%3D1)%5C%5C%0A%26%3D%26P%5Cbigg(%5Cbigcap_%7Bp:%7B%5Crm%20prime%7D%7DE_p%5Ec%5Cbigg)%5C%5C%0A%26%3D%26%5Cprod_%7Bp:%7B%5Crm%20prime%7D%7D(1-P(E_p))%5C%5C%0A%26%3D%26%5Cprod_%7Bp:%7B%5Crm%20prime%7D%7D(1-1/p%5Es).png)
%5C%5C%0A%26%3D%26P(E_%7Bi_1%7D%5Ccap%5Ccdots%20E_%7Bi_p%7D)P(F_%7Bi_1%7D%5Ccap%20%5Ccdots%20%5Ccap%20F_%7Bi_p%7D)%5Cquad%20(X,Y:%20%7B%5Crm%20independent%7D).png)
%3DP(X%3Dkp)/P(E_p)%3DP(X%3Dk).png)
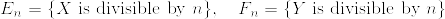
%26%3D%26P%5Cbigg(E_n%5Ccap%20F_n%5Ccap%20%5Cbigcap_%7Bp:%7B%5Crm%20prime%7D%7D(E_%7Bnp%7D%5Ccap%20F_%7Bnp%7D)%5Ec%20%5Cbigg)%5C%5C%0A%26%3D%26E%5Cbigg[1_%7BE_n%5Ccap%20F_n%7DP%5Cbigg(%5Cbigcap_%7Bp:%7B%5Crm%20prime%7D%7D(E_%7Bnp%7D%5Ccap%20F_%7Bnp%7D)%5Ec%7CE_n,F_n%5Cbigg)%5Cbigg]%5C%5C%0A%26%3D%26E[1_%7BE_n%7D1_%7BF_n%7DP(H%3D1)]%5C%5C%0A%26%3D%26n%5E%7B-2s%7D/%5Czeta(2s).png)
%3D%5Cprod_%7Bp:%7B%5Crm%20prime%7D%7D(p1_%7BE_p%7D1_%7BF_p%7D+%5Cmax%20%5C%7B1_%7BE_p%5Ec%7D,1_%7BF_p%5Ec%7D%5C%7D).png)
%3D1/%5Czeta(2s).png)
.png)
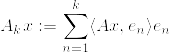
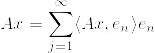
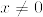
x%7C%5E2%26%3D%26%5Clim_%7BN%5Cto%5Cinfty%7D%5Csum_%7Bn%3Dk+1%7D%5E%7BN%7D%7C%5Clangle%20Ax,e_n%5Crangle%7C%5E2%5C%5C%0A%26%3D%26%5Clim_%7BN%5Cto%5Cinfty%7D%5Csum_%7Bn%3Dk+1%7D%5E%7BN%7D%7C%5Clangle%20x,A%5E*e_n%5Crangle%7C%5E2%5Cquad%20(A%5E*:%20%7B%5Crm%20adjoint~operator%7D)%5C%5C%0A%26%5Cleq%20%26%5Clim_%7BN%5Cto%5Cinfty%7D%7Cx%7C%5E2%5Csum_%7Bn%3Dk+1%7D%5E%7BN%7D%7CA%5E*e_n%7C%5E2%5C%5C%0A%26%3D%26%7Cx%7C%5E2%5Csum_%7Bn%3Dk+1%7D%5E%7B%5Cinfty%7D%7CA%5E*e_n%7C%5E2.png)