多様体上の調和関数
Mをコンパクト,連結,向きづけられた境界付き可微分多様体とする.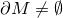 であるとする.M上の調和関数u,vが境界上で一致するときuとvはM上で一致する.
であるとする.M上の調和関数u,vが境界上で一致するときuとvはM上で一致する.
という主張の証明のメモ.
u-vを考えれば良いから,調和関数fで境界上で0となるものが,M上で恒等的に0になることを示せばよい.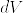 をMの体積要素とする.Stokesの定理から
をMの体積要素とする.Stokesの定理から
ただし境界にはMから定まる向きを入れ,Nは外向きの単位ベクトルとし,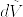 は境界の体積要素とする.fは調和で境界上で0となるから
は境界の体積要素とする.fは調和で境界上で0となるから
よって 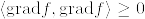 より
より 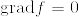 .ゆえにfは定数関数(任意のベクトル場Xに対してXf=0より).仮定より境界上で0で,Mは連結であったからf=0となる.
.ゆえにfは定数関数(任意のベクトル場Xに対してXf=0より).仮定より境界上で0で,Mは連結であったからf=0となる.
似たような主張で「Mの境界が空であったら調和関数は定数に限る(Mは向き付可能でなくても良い)」というのが松島多様体にあった.そちらもgrad fが0となることを示すために 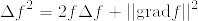 という式をつかい,ストークスの定理から導いていた.細かいけど
という式をつかい,ストークスの定理から導いていた.細かいけど 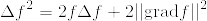 ではないだろうか.計算すると
ではないだろうか.計算すると
よって
となるから
となる気がするのだけど・・・
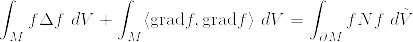
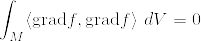
.png)
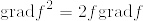
%3D2f%5CDelta%20f+2%7C%7C%7B%5Crm%20grad%7Df%7C%7C%5E2.png)