Levy's Characterization の反例っぽいもの(反例ではない)
Exercise3.3.17
%7D,W_t%5E%7B(2)%7D,W_t%5E%7B(3)%7D).png)
を3次元の0を出発するブラウン運動とし，
%7D).png)
%7D_t:%3DW_t%5E%7B(1)%7D,%5Cquad%20M_t%5E%7B(2)%7D:%3DW_t%5E%7B(2)%7D,%5Cquad%20M_t%5E%7B(3)%7D%3DXW_t%5E%7B(3)%7D.png)
とおく．このとき，どの二つのペア %7D,M%5E%7B(2)%7D),%5Cquad%20(M%5E%7B(1)%7D,M%5E%7B(3)%7D),%5Cquad%20(M%5E%7B(2)%7D,M%5E%7B(3)%7D).png)
も2次元のブラウン運動になるが，%7D,M%5E%7B(2)%7D,M%5E%7B(3)%7D).png)
は3次元のブラウン運動にならないことを示せ．またこれが，Levy's Characterization Theoremに矛盾しない理由を説明せよ．つまり，%7D,M%5E%7B(j)%7D%5Crangle_t%3D%5Cdelta_%7Bij%7Dt%5Cquad%20(i,j%3D1,2,3).png)
で %7D%5Cquad%20(i%3D1,2,3).png)
は局所連続マルチンゲールであるが， は3次元のブラウン運動にならないのは矛盾でないのはなぜか．
[証明]
第1段
%7D_t.png)
がブラウン運動であることを示す．そのために次の補題を用いる．(R.Durrett「Probability Theory and Examples」,4th-Edition,p302,303)
補題
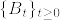がブラウン運動であることと，以下の3条件を満たすことは同値である．
(i)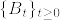 はガウス過程である．
(ii)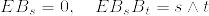
(iii)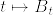 
は確率1で連続．
この補題より はブラウン運動である．実際(i)を満たすことは .png)
と %5Cquad%20(j%3D1,2,%5Cldots,n).png)
に対して
%7D%5Cin%20A_%7Bt_1%7D,%5Cldots,M_%7Bt_n%7D%5E%7B(3)%7D%5Cin%20A_%7Bt_n%7D)%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B2%7DP(W_%7Bt_1%7D%5E%7B(3)%7D%5Cin%20A_%7Bt_1%7D,%5Cldots,W_%7Bt_n%7D%5E%7B(3)%7D%5Cin%20A_%7Bt_n%7D)+%5Cfrac%7B1%7D%7B2%7DP((-W_%7Bt_1%7D%5E%7B(3)%7D)%5Cin%20A_%7Bt_1%7D,%5Cldots,(-W_%7Bt_n%7D%5E%7B(3)%7D)%5Cin%20A_%7Bt_n%7D)%5C%5C%0A%26%3D%26P(W_%7Bt_1%7D%5E%7B(3)%7D%5Cin%20A_%7Bt_1%7D,%5Cldots,W_%7Bt_n%7D%5E%7B(3)%7D%5Cin%20A_%7Bt_n%7D).png)
上の式変形はXの値で分割して考えると得られる．また(ii)を満たすことは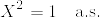
より従う．また(iii)は明らか．よってこの補題より はブラウン運動である．
第2段
が2次元のブラウン運動であることを示す． %7D,M%5E%7B(2)%7D).png)
が2次元のブラウン運動であることは明らか． %7D,M%5E%7B(3)%7D).png)
が2次元のブラウン運動であることを示す．そのためには %7D_t-M%5E%7B(1)%7D_s.png)
と %7D_t-M%5E%7B(3)%7D_s.png)
が独立であることを示せばよい．それには任意のボレル集合A_1,A_2に対して
%7D-M_s%5E%7B(1)%7D)%5Cin%20A_1,(M_t%5E%7B(3)%7D-M_s%5E%7B(3)%7D)%5Cin%20A_2)%5C%5C%0A%26%3D%26P((M_t%5E%7B(1)%7D-M_s%5E%7B(1)%7D)%5Cin%20A_1)P((M_t%5E%7B(3)%7D-M_s%5E%7B(3)%7D)%5Cin%20A_2).png)
が成立することを言えばよいが，それは上と同様にXの値で場合分けすれば示せる．同様にして %7D,M%5E%7B(3)%7D).png)
も2次元のブラウン運動である．
第3段
が3次元のブラウン運動でないことを示す．背理法による．ブラウン運動であると仮定する．このとき
%7DM_1%5E%7B(2)%7DM_1%5E%7B(3)%7D%3D%7CW_1%5E%7B(1)%7DW_1%5E%7B(2)%7DW_1%5E%7B(3)%7D%7C%5Cgeq%200.png)
・・・(1)
よって
%7DM_1%5E%7B(2)%7DM_1%5E%7B(3)%7D]%5Cgeq%200.png)
一方 は0を出発するブラウン運動であるから，%7D,M_1%5E%7B(2)%7D,M_1%5E%7B(3)%7D.png)
は独立．したがって
%7DM_1%5E%7B(2)%7DM_1%5E%7B(3)%7D]%3D%5Cprod_%7Bj%3D1%7D%5E3EM_1%5E%7B(j)%7D%3D0.png)
・・・(2)
よって(1),(2)式より
%7DM_1%5E%7B(2)%7DM_1%5E%7B(3)%7D%3D0%5Cquad%20%7B%5Crm%20a.s.%7D.png)
がブラウン運動であるとすると，
%7DM_1%5E%7B(2)%7DM_1%5E%7B(3)%7D%3D0)%5Cleq%20%5Csum_%7Bj%3D1%7D%5E3P(M_1%5E%7B(j)%7D%3D0)%3D0.png)
よって矛盾である．
第4段
Levy's Characterization Theoremに矛盾しない理由はフィルトレーションにある．つまり各過程が適合しているフィルトレーションに違いがあるので矛盾しない．[証明終]
長くなったので第4段についてはまた次の記事で書こうと思います．あとKaratzas＆ShreveのBrownian Motion and Stochastic Calculusの本の問題は別のカテゴリ[KaratzasAndShreve]にすることにしました．
