一様可積分かつ局所連続マルチンゲールであるがマルチンゲールでない例2(M.Yor)
一様可積分かつ局所連続マルチンゲールであるがマルチンゲールでない例(M.Yor)
上の記事で一様可積分かつ局所連続マルチンゲールであるがマルチンゲールでない例を調べたのですが,からしゅれでは次のExerciseでまたこれと同じ種類の例を挙げているので,証明します.
Exercise3.3.37
Rを0を出発する2次元のベッセル過程とする.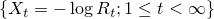 が局所連続マルチンゲールで
が局所連続マルチンゲールで
が成立することを示せ.また 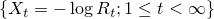 はマルチンゲールでないことも示せ.(一様可積分であることもわかる.)
はマルチンゲールでないことも示せ.(一様可積分であることもわかる.)
[証明]
まず局所連続マルチンゲールであることを示す.伊藤の公式から
これより 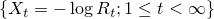 は局所連続マルチンゲールである.ただしBは1次元の標準ブラウン運動である.
は局所連続マルチンゲールである.ただしBは1次元の標準ブラウン運動である.
ただしn次元球の体積を用いて積分を評価した(一様可積分かつ局所連続マルチンゲールであるがマルチンゲールでない例(M.Yor)参照).α<0のときは, .png) として
として
これより
となる.次に一様可積分であることを示す.そのために任意の 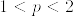 に対してL^p有界であることを示す.つまり
に対してL^p有界であることを示す.つまり
を示す.
よって
となる.これより一様可積分である.最後にマルチンゲールでないことを背理法を用いて示す.マルチンゲールであれば期待値が一定であるから
.png)
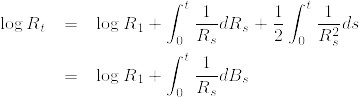
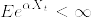
%5C%5C%0A%26%3D%26%5Cint_0%5E%5Cinfty%20%5Calpha%20y%5E%7B%5Calpha%20-1%7DP(1/R_t%3Ey)dy%20%5C%5C%0A%26%5Cleq%20%261+%5Cint_1%5E%7B%5Cinfty%7D%5Calpha%20y%5E%7B%5Calpha%20-1%7D%5Cfrac%7B1%7D%7B2%5Cpi%20t%7D%5Cfrac%7B%5Cpi%7D%7By%5E2%7Ddy%5C%5C%0A%26%3D%261+%5Cfrac%7B%5Calpha%20%7D%7B2t(2-%5Calpha%20)%7D%3C%5Cinfty%5Cquad%20%5Cforall%7Bt%7D%5Cgeq%201.png)
drd%5Ctheta%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B2t%7D%5Cint_0%5E%7B%5Cinfty%7Ds%5E%7B(%5Cbeta/2+1)-1%7D%5Cexp%20%5Cbigg(-%5Cfrac%7Bs%7D%7B2t%7D%5Cbigg)dr%5Cquad%20(s%3Dr%5E2)%5C%5C%0A%26%3D%26%5Cfrac%7B%5CGamma%20(%5Cbeta%20/2+1)%7D%7B(2t)%5E%7B%5Cbeta%20/2+2%7D%7D%3C%5Cinfty%0A.png)
%3C%5Cinfty%20%5Cquad%20(1%3C%5Cforall%7Bp%7D%3C2).png)
%26%3D%26%5Cint_0%5E%7B%5Cinfty%7Dpy%5E%7Bp-1%7DP(%7CX_t%7C%3Ey)dy%5C%5C%0A%26%5Cleq%20%26%5Cint_0%5E%7B%5Cinfty%7Dpy%5E%7Bp-1%7D%5Cexp(-py)E(%5Cexp(%7CpX_t%7C))dy%5C%5C%0A%26%5Cleq%20%26%20p(E(%5Cexp(pX_t))+E(%5Cexp(-pX_t))%5Cint_0%5E%7B%5Cinfty%7Dy%5E%7Bp-1%7D%5Cexp(-py)dy%5C%5C%0A%26%5Cleq%20%26%20p%5Cbigg(1+%5Cfrac%7Bp%7D%7B2t(2-p)%7D+%5Cfrac%7B%5CGamma%20(p/2+1)%7D%7B(2t)%5E%7Bp/2+2%7D%7D%5Cbigg)%5Cfrac%7B%5CGamma%20(p)%7D%7Bp%5Ep%7D%5C%5C%0A%26%5Cleq%20%26%20%5Cbigg(1+%5Cfrac%7Bp%7D%7B2(2-p)%7D+%5CGamma%20(p/2+1)%5Cbigg)%5Cfrac%7B%5CGamma%20(p)%7D%7Bp%5E%7Bp-1%7D%7D%3C%5Cinfty%20%5Cquad%20(t%5Cgeq%201).png)
%5C%5C%0A%26%3D%26%20%5Cint_%7B%5Ctheta%20%3D0%7D%5E%7B%5Ctheta%20%3D%202%5Cpi%7D%5Cint_%7Br%3D0%7D%5E%7Br%3D%5Cinfty%7D(-r%5Clog%20r)%5Cfrac%7B1%7D%7B2%5Cpi%20t%7D%5Cexp%20%5Cbigg(%20-%5Cfrac%7Br%5E2%7D%7B2t%7D%5Cbigg)drd%5Ctheta%5C%5C%0A%26%5Cleq%20%26%5Cfrac%7B1%7D%7Bte%7D%5Cint_%7B0%7D%5E%7B%5Cinfty%7D%5Cexp%5Cbigg(-%5Cfrac%7Br%5E2%7D%7B2t%7D%5Cbigg)dr%5C%5C%0A%26%3D%26%5Cfrac%7B%5Csqrt%7B2%5Cpi%7D%7D%7B2e%5Csqrt%7Bt%7D%7D.png)

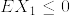

dr%5C%5C%0A%26%5Cgeq%20%26-%5Cint_0%5E%7B%5Cinfty%7Dr(r-1)%5Cexp(-r%5E2/2)dr%5C%5C%0A%26%3D%26-%5Cint_0%5E%7B%5Cinfty%7Dr%5E2%5Cexp(-r%5E2/2)dr+%5Cint_0%5E%7B%5Cinfty%7D%20r%5Cexp(-r%5E2/2)dr%5C%5C%0A%26%3D%26-%5Cfrac%7B1%7D%7B2%7D%5Cint_0%5E%7B%5Cinfty%7D%5Csqrt%7Bs%7D%5Cexp(-s/2)ds+1%5Cquad%20(s%3Dr%5E2)%5C%5C%0A%26%3D%26-%5Cfrac%7B%5CGamma%20(3/2)%7D%7B2%5E%7B3/2%7D%7D+1%5C%5C%0A%26%3D%26-%5Cfrac%7B%5Csqrt%7B%5Cpi%7D%7D%7B4%5Csqrt%7B2%7D%7D+1%3E0.png)