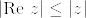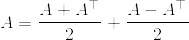Ostrowski-Taussky Inequality
Ostrowski-Taussky Inequality
Aを正方行列とし,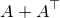 が正定値行列であるとする.このとき以下の不等式が成立する:
が正定値行列であるとする.このとき以下の不等式が成立する:
となっている.このような行列に関して次の不等式が成立する(下の補第参照):
これが成り立てば
これより証明が終わる.あとは次の補題1を示せばよい.ただし帰納法の成立のため主張を拡張する.
補第1
証明
Bの次元に関する帰納法で示す.n=1のときは明らかに成立する.n=k-1のとき成立するとする.まず次のように行列Bを分割する.
ここでCは(k-1)×(k-1)行列である.まず任意の%5E%7B%5Ctop%7D%5Cin%5Cmathbf%7BR%7D%5En.png) に対して,
に対して,%5E%7B%5Ctop%7D.png) として,
として,
となることがまずわかる.
次に, よりブロック行列の行列式を考えれば
よりブロック行列の行列式を考えれば
帰納法の仮定からCは正則であるから,Sherman-Morrison-Woodburyの公式より
ここで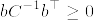 であることがわかる.実際帰納法の仮定より
であることがわかる.実際帰納法の仮定より
Cは正則だから任意のxに対してあるyがあって
よって任意のxに対して
となるためである.これより
[証明終]
主張が言いたいことを考えると,これは複素数zに対する不等式
の行列への拡張ではないかという指摘を受けました.というのも
と分けます.右辺の第一項はAを対称化したもので,第二項は反対称化したものです.実対称行列の固有値は実数で,反対称行列の固有値は純虚数です.つまり固有値の視点から見ると,上の分解は行列の実部と虚部への分解に対応するものではないかと考えられます.そうすると主張の左辺はAの固有値の実部の積,右辺は固有値の絶対値の積なので,不等号が成り立つと思われます.これを正当化するには,右辺の第一項と第二項が同時三角化可能で,行列の和の固有値が,各行列の固有値の和になることを言わないとダメだと思いますが...
ちなみに主張の右辺の絶対値は要らないことが証明から分かります.
%5Cleq%20%7C%5Cdet(A)%7C..png)
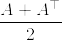
P%3D%7B%5Crm%20diag%7D[%5Clambda_1,%5Cldots,%5Clambda_n],%5Cquad%20%5Clambda_i%3E0~(i%3D1,2,%5Cldots,n).png)
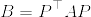
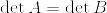
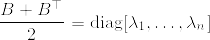
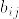
%5C%5C%0A-b_%7Bji%7D%20%26%20(i%5Cneq%20j)%0A%5Cend%7Barray%7D%0A%5Cright..png)

%26%3D%26%5Cdet(%7B%5Crm%20diag%7D[%5Clambda_1,%5Cldots,%5Clambda_n])%5C%5C%0A%26%3D%26%5Cprod_%7Bi%3D1%7D%5En%5Clambda_i%5C%5C%0A%26%5Cleq%20%26%5Cdet%20B%5C%5C%0A%26%3D%26%5Cdet%20A..png)
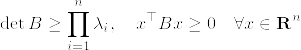
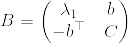
%5E2+(%5Chat%7Bx%7D%5E%7B%5Ctop%7DC%5Chat%7Bx%7D)%5Cgeq%200.png)
..png)
%3D%5Clambda_1(1+bC%5E%7B-1%7Db%5E%7B%5Ctop%7D)%5Cdet%20C%5C%5C%0A.png)
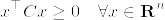
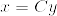
%5E%7B%5Ctop%7D%5C%5C%0A%26%3D%26y%5E%7B%5Ctop%7DCy%5Cgeq%200.png)
%5Cdet%20C%5C%5C%0A%26%5Cgeq%20%26%5Clambda_1%5Cdet%20C%5C%5C%0A%26%5Cgeq%20%26%5Cprod_%7Bi%3D1%7D%5En%5Clambda_i..png)