class DL
からしゅれに右連続非負値submartingaleはclass DLであるという主張があって,同様に右連続martingaleもclass DLとなることが言える.
証明
a>0を固定し,%3D1.png) となるstopping timeの族を
となるstopping timeの族を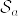 とする.定義より
とする.定義より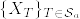 が一様可積分であることを示せばよい.Jensenの不等式より
が一様可積分であることを示せばよい.Jensenの不等式より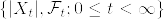 はsubmartingale. OSTより
はsubmartingale. OSTより
またチェビシェフの不等式より
よって積分の絶対連続性より
これより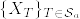 は一様可積分.(証明終)
は一様可積分.(証明終)
Xが発展的可測のとき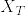 は
は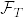 可測だけど,からしゅれだとadaptedしか仮定していないのに大丈夫か?という疑問が起きた.けれど,右連続性からXはmeasurableで,さらにadaptedと右連続性から発展的可測がでるから,結局発展的可測を仮定しているのと同じことなので,問題なかった.というかもっと早くこの疑問を持つべきだった.あまり発展的可測は強い条件じゃないのかもしれない.
可測だけど,からしゅれだとadaptedしか仮定していないのに大丈夫か?という疑問が起きた.けれど,右連続性からXはmeasurableで,さらにadaptedと右連続性から発展的可測がでるから,結局発展的可測を仮定しているのと同じことなので,問題なかった.というかもっと早くこの疑問を持つべきだった.あまり発展的可測は強い条件じゃないのかもしれない.
可分距離空間上のtightでない確率測度の例(つづき)
可分距離空間上のtightでない確率測度の例 でルベーグ外測度1,ルベーグ内測度0の集合の存在を認めたのですが,[0,1]の部分集合A,Bでdisjointかつともにルベーグ外測度が1であるようなルベーグ非可測集合の存在を教えていただきました.
詳しくは
を見ていただきたいと思います.
可分距離空間上のtightでない確率測度の例
完備可分距離空間上では確率測度の族 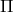 がtightであることと,相対コンパクトであることは同値.けれども可分距離空間上の確率測度でtightでないものが存在する(よって相対コンパクトであるがtightでない例になっている).
がtightであることと,相対コンパクトであることは同値.けれども可分距離空間上の確率測度でtightでないものが存在する(よって相対コンパクトであるがtightでない例になっている).
この例はBillingsleyの Convergence of Probability Measures の章末問題として載っていた例です.
 | Convergence of Probability Measures (Wiley Series in Probability and Statistics) (1999/07/30) Patrick Billingsley 商品詳細を見る |
まず [0,1] の部分集合 S をルベーグ外測度が1,ルベーグ内測度が0であるようなルベーグ非可測集合とする(存在は認める).この集合 S に [0,1] の相対位相を入れると,可分距離空間となる([0,1]の開基の元とSの共通部分から(あれば)一点とって集めた集合Aは可算集合でSで稠密).またルベーグ外測度 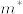 を S に制限したものを
を S に制限したものを 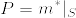 とおく.Pは外測度の性質を満たし,カラテオドリの意味で可測な集合全体
とおく.Pは外測度の性質を満たし,カラテオドリの意味で可測な集合全体 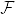 の上の測度となる.また明らかに,任意のルベーグ可測集合 E に対して
の上の測度となる.また明らかに,任意のルベーグ可測集合 E に対して 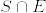 は P可測集合である.さらにSのルベーグ外測度は1なので,PはSの上の確率測度となる.
は P可測集合である.さらにSのルベーグ外測度は1なので,PはSの上の確率測度となる.
ここで S の任意のコンパクト集合 K に対して P(K)=0 であることを示す(これよりPはtightでない S の上の確率測度となる).包含写像 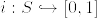 は連続.よって i(K) は [0,1] のコンパクト集合.よって K は [0,1] のコンパクト集合.ここで 内測度の定義から
は連続.よって i(K) は [0,1] のコンパクト集合.よって K は [0,1] のコンパクト集合.ここで 内測度の定義から
Billingsleyはさらに可分距離空間上の確率測度の族で,相対コンパクトかつ各確率測度はtightだが,族はtightでないものも構成していて,証明できたらまたブログに書こうと思います.
しかし自分でもいろいろ考えてみたけど,ルベーグ非可測集合とは・・・
X,Yは実確率変数とし,任意の実数aに対しP(X=a)=0,またXとYは独立で同分布に従うとする.このときP(X=Y)=0となる.
タイトルの主張は確率論のテストで必要だった主張です.テストの時は分かりませんでした.
ですが,零集合の非可算和は零集合とは限らないのでこれではうまくいかないです.
そこでFubiniの定理を使います.P^Xを像測度とするとき,XとYは独立であるから, %7D%3DP%5EX%5Cotimes%20P%5EY.png) であり,非負値可測関数に対してFubiniの定理がなりたつから
であり,非負値可測関数に対してFubiniの定理がなりたつから
となる.
であるから
となる.
Sardの定理の証明を読んでいて,R^nの部分集合Aが,任意の超平面{p}×R^{n-1}と共通部分をとったとき,そのn-1次元ルベーグ測度が0ならば,Aのn次元ルベーグ測度が0 というのをFubiniの定理から示していて,それのおかげでやっと解決しました.
どうでもいいのですがミルナーの本は添字が見づらいです.
a.s.収束と位相
Durrettの本に
Since there is a sequence of random variables that converges in probability but not a.s. , it follows that a.s. convergence does not come from a metric, or even from a topology.
とあった.
確率論の授業でも紹介されてた主張で,どう示すのかなと思っていたのだけれど,Durrettでは
Let 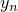 be a sequence of elements of a topological space. If every subsequence
be a sequence of elements of a topological space. If every subsequence %7D%0A.png) has a further subsequence
has a further subsequence %7D%0A.png) that converges to y then
that converges to y then  .
.
という主張から導けると書いてあった.
これからもしa.s.収束がある位相で定まると仮定して矛盾が導ける.確率収束する列から任意に部分列(確率収束する)をとって,Borel-Cantelliの補題からその確率収束先に概収束する部分列を取れる.概収束が位相から定まるという仮定と上の主張から,もとの確率収束する列は概収束する.これは矛盾.
という感じになる.

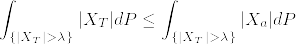
%5Cleq%20%5Cfrac%7BE(%7CX_a%7C)%7D%7B%5Clambda%7D.png)
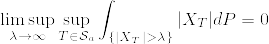
%3D%5Csup%20%5C%7B%20m%5E*(A)%20:%20A%20%7B%5Crm%5C%20is%5C%20a%5C%20compact%5C%20set%5C%20in%5C%20[0,1]%7D,%20A%5Csubset%20S%20%5C%7D.png)
%3D0.png)
%3Dm%5E*(K)%3D0.png)
%3DP(%5Cbigcup_%7Ba%5Cin%20%5Cmathbf%7BR%7D%7D%20%5C%7B%20X%3DY%3Da%20%5C%7D%20).png)
%26%3D%26%5Cint_%7B%5COmega%7D1_%7B%5C%7BX%3DY%5C%7D%7D(%5Comega)dP(%5Comega)%5C%5C%0A%26%3D%26%5Cint_%7B%5Cmathbf%7BR%7D%7D%5Cbigg(%5Cint_%7B%5Cmathbf%7BR%7D%7D1_%7B%5C%7Bx%3Dy%5C%7D%7D(x,y)dP%5EX(x)%5Cbigg)dP%5EY(y).png)
dP%5EX(x)%3DP(X%3Dy)%3D0.png)
%3D%5Cint_%7B%5Cmathbf%7BR%7D%7D%5C%200%5C%20dP%5EY(y)%3D0.png)
%3D%5Csup%5C%7By%5Cin%5Cmathbf%7BR%7D:F(y)%5Cleq%5Comega%5C%7D.png)
%5Cleq%20a%5CLongleftrightarrow%20x%5Cleq%20Y(a).png)
%3E%20a%5CLongleftrightarrow%20x%3E%20Y(a).png)
.png)
%3CY(%5Comega).png)
)%5Cgeq%20F(Y(%5Comega_n))%5Cgeq%20%5Comega_n%20.png)
)%3C%20%5Comega.png)