モーメント母関数の条件付き期待値
次の記事でKaratzasAndShreveのProblem3.2.28の証明をしたいと思いますが,そこで使う補題を示しておこうと思います.
主張
.png) を確率空間とし,
を確率空間とし,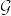 を
を 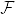 の部分σ加法族とする. また
の部分σ加法族とする. また 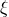 をほとんど確実に有界な
をほとんど確実に有界な 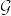 可測関数とし,
可測関数とし, 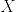 を平均 0 分散 t の正規分布に従う
を平均 0 分散 t の正規分布に従う 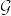 と独立な確率変数とする.このとき
と独立な確率変数とする.このとき
が成立する.つまり 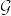 で条件付けると
で条件付けると 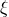 を定数と見なした
を定数と見なした 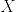 のモーメント母関数になっている.
のモーメント母関数になっている.
よって
となる.次に 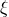 がほとんど確実に有界な一般の確率変数のときに示す.このとき単関数の列
がほとんど確実に有界な一般の確率変数のときに示す.このとき単関数の列 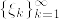 で
で
となるものが存在する.ここで
とすると,Vは可測である.さらに
であり,
である.よって条件付き期待値の優収束定理より
を得る.[証明終]
もっと簡単に示せそうな気もするんですが,とりあえず上のように愚直に示しました.あと細かい議論は抜きで条件付き期待値と可算和を交換しようとすると
途中で
であることを使いました.これでも期待値と和の交換の正当性が言えればいいと思います.
exponential supermartingale
Problem3.2.28
 をstandard Brownian motion とし
をstandard Brownian motion とし 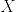 をmeasurable,adaptedで
をmeasurable,adaptedで
を満たす確率過程とする.つまり確率積分
は定義できるものとする.このとき
と定義する. ),%5Cmathcal%7BF%7D_t;0%5Cleq%20t%3C%5Cinfty%5C%7D.png) は優マルチンゲールであることを示せ.また
は優マルチンゲールであることを示せ.また 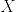 が単過程のときマルチンゲールであることを示せ.
が単過程のときマルチンゲールであることを示せ.
[証明]
まず 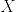 が単過程のときマルチンゲールであることを示す.
が単過程のときマルチンゲールであることを示す. 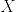 が単過程のとき
が単過程のとき 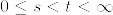 に対して
に対して
と表せる.ただし 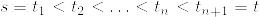 とした.また単過程の定義よりある定数Mが存在して
とした.また単過程の定義よりある定数Mが存在して
であり, 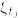 は
は 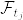 可測である.前の記事の補題より
可測である.前の記事の補題より
これと条件付き期待値のtower propertyから
が成立する.よって
これより 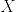 が単過程のときマルチンゲールである.
が単過程のときマルチンゲールである.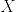 が単過程でないときは伊藤の公式より
が単過程でないときは伊藤の公式より
よって ),%5Cmathcal%7BF%7D_t;0%5Cleq%20t%3C%5Cinfty%5C%7D.png) は非負値局所連続マルチンゲールである.一般に非負値局所連続マルチンゲールは優マルチンゲールであるから(KaratzasAndShreve, Problem1.5.19),証明が終わる.[証明終]
は非負値局所連続マルチンゲールである.一般に非負値局所連続マルチンゲールは優マルチンゲールであるから(KaratzasAndShreve, Problem1.5.19),証明が終わる.[証明終]
Xが単過程でないときは,Xを単過程でうまく近似して(KaratzasAndShreve, Problem3.2.27)Fatouの補題を使うことでも示せますが,準備が大変なので伊藤の公式をつかった証明で済ませました.また省略しましたが条件付き期待値のところで可測なものを外に出していますが,可積分性をチェックしなければいけません.それは 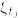 の有界性から従います.
の有界性から従います.
[追記] 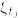 の有界性から議論するのではなく先に優マルチンゲールであることを言って
の有界性から議論するのではなく先に優マルチンゲールであることを言って
を言うのが早い気がしました.
%7C%5Cmathcal%7BG%7D]%3D%5Cexp%5Cbigg(%5Cfrac%7B1%7D%7B2%7D%5Cxi%5E2t%5Cbigg)%5Cquad%20%7B%5Crm%20a.s.%7D.png)
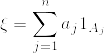
.png)
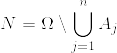
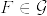
dP%26%3D%26%5Csum_%7Bj%3D1%7D%5En%5Cint_%7BF%5Ccap%20A_j%7D%5Cexp(a_jX)dP+P(F%5Ccap%20N)%5C%5C%0A%26%3D%26%20%5Csum_%7Bj%3D1%7D%5En%20%5Cexp%5Cbigg(%20%5Cfrac%7B1%7D%7B2%7Da_j%5E2t%5Cbigg)P(A_j%5Ccap%20F)+P(F%5Ccap%20N).png)
dP%3D%5Csum_%7Bj%3D1%7D%5En%5Cexp%5Cbigg(%5Cfrac%7B1%7D%7B2%7Da_j%5E2t%5Cbigg)P(A_j%5Ccap%20F)+P(F%5Ccap%20N).png)
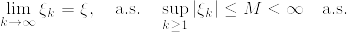
%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Cexp(M%7CX(%5Comega)%7C)+1.png)
%20X(%5Comega))%5Cleq%20V(%5Comega)%5Cquad%20%7B%5Crm%20a.s.%7D.png)
%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%20t%7D%7D%5Cexp(-%5Cfrac%7Bx%5E2%7D%7B2t%7D)dx+1%5C%5C%0A%26%5Cleq%262%5Cint_%7B%5Cmathbf%7BR%7D%7D%5Cexp(Mx)%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%20t%7D%7D%5Cexp(-%5Cfrac%7Bx%5E2%7D%7B2t%7D)dx%20+1%5C%5C%0A%26%3D%26%5Cexp%5Cbigg(%5Cfrac%7BM%5E2t%7D%7B2%7D%5Cbigg)%20+1%3C%5Cinfty.png)
%7C%5Cmathcal%7BG%7D]%26%3D%26%5Clim_%7Bn%5Cto%5Cinfty%7DE[%5Cexp(%5Cxi_n%20x)%7C%5Cmathcal%7BG%7D]%5C%5C%0A%26%3D%26%5Clim_%7Bn%5Cto%5Cinfty%7D%5Cexp%5Cbigg(%5Cfrac%7B1%7D%7B2%7D%5Cxi_n%5E2t%5Cbigg)%5C%5C%0A%26%3D%26%5Cexp%5Cbigg(%5Cfrac%7B1%7D%7B2%7D%5Cxi%5E2t%5Cbigg)%5Cquad%20%7B%5Crm%20a.s.%7D.png)
%7C%5Cmathcal%7BG%7D]%26%3D%26%5Csum_%7Bj%3D0%7D%5E%7B%5Cinfty%7D%5Cfrac%7B%5Cxi%5Ej%7D%7Bj!%7DE[X%5Ej%7C%5Cmathcal%7BG%7D]%5C%5C%0A%26%3D%26%5Csum_%7Bj%3D0%7D%5E%7B%5Cinfty%7D%5Cfrac%7B%5Cxi%5Ej%7D%7Bj!%7DE[X%5Ej]%5Cquad%20(%7B%5Crm%20independent%7D)%5C%5C%0A%26%3D%261+%5Csum_%7Bj%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B%5Cxi%5E%7B2j%7D%7D%7B(2j)!%7D%5Cfrac%7B(2j)!%7D%7B2%5Ejj!%7Dt%5E%7Bj%7D%5C%5C%0A%26%3D%261+%5Csum_%7Bj%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7Bj!%7D%5Cbigg(%5Cfrac%7B%5Cxi%5E2%20t%7D%7B2%7D%5Cbigg)%5Ej%5C%5C%0A%26%3D%26%5Cexp%5Cbigg(%5Cfrac%7B1%7D%7B2%7D%5Cxi%5E2t%5Cbigg).png)
!%7D%7B2%5Ejj!%7Dt%5Ej,%5Cquad%20E[X%5E%7B2j+1%7D]%3D0.png)
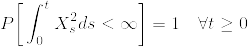
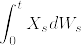
%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Cint_0%5Et%20X_sdW_s-%5Cfrac%7B1%7D%7B2%7D%5Cint_0%5EtX_s%5E2ds.png)
-%5Czeta_s(X))%7C%5Cmathcal%7BF%7D_s]%3D1%5Cquad%20%7B%5Crm%20a.s.%7D.png)
-%5Czeta_s(X))%3D%5Cexp%5Cbigg%5C%7B%5Csum_%7Bj%3D1%7D%5En%5Cbigg%5C%7B%5Cxi_%7Bt_j%7D(W_%7Bt_%7Bj+1%7D%7D-W_%7Bt_j%7D)-%5Cfrac%7B1%7D%7B2%7D%5Cxi_%7Bt_j%7D%5E2(t_%7Bj+1%7D-t_j)%20%5Cbigg%5C%7D%5Cbigg%5C%7D.png)
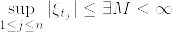
)%7C%5Cmathcal%7BF%7D_%7Bt_j%7D]%3D%5Cexp%5Cbigg(%5Cfrac%7B1%7D%7B2%7D%5Cxi_%7Bt_j%7D%5E2(t_%7Bj+1%7D-t_j)%5Cbigg).png)
)%7C%5Cmathcal%7BF%7D_s]%26%3D%26%5Cexp(%5Czeta_s(X))E[%5Cexp(%5Czeta_t(X)-%5Czeta_s(X))%7C%5Cmathcal%7BF%7D_s]%5C%5C%0A%26%3D%26%5Cexp(%5Czeta_s(X))%5Cquad%20%7B%5Crm%20a.s.%7D.png)
)%3D1+%5Cint_0%5Et%5Cexp(%5Czeta_s(X))X_sds.png)
)]%5Cleq%201.png)
-%5Czeta_s(X))]%5Cleq%20%5Csqrt%7BE[%5Cexp(2%5Czeta_t(X))]%7D%5Csqrt%7BE[%5Cexp(2%5Czeta_s(X))]%7D%5Cleq%201.png)