Problem3.5.7
Problem3.5.7
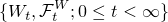 を一次元のブラウン運動とする.ただしフィルとレーションはWを可測にする最小のσ加法族とする.Tを
を一次元のブラウン運動とする.ただしフィルとレーションはWを可測にする最小のσ加法族とする.Tを.png) -stopping time でかつ,
-stopping time でかつ,%3D1.png) を満たすものとする.このときWaldの恒等式
を満たすものとする.このときWaldの恒等式
が成立することと,
として定義したものを 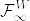 に一意的に拡張した測度である(Karatzas and Shreve, Corollary 3.5.2参照).
に一意的に拡張した測度である(Karatzas and Shreve, Corollary 3.5.2参照).
は上の条件を満たす.(Novikov conditionの証明に用いられる(Proposition 3.5.12))
[証明]
Optional Sampling Theoremから
よって単調収束定理から
特に, なら
なら  なので
なので %5Cleq%20P(S_b%3C%5Cinfty)%3D1.png) で
で %7D.png) のもとで,
のもとで,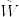 はブラウン運動になる(Girsanovの定理)ので
はブラウン運動になる(Girsanovの定理)ので
[証明終]
Exercise3.5.10
Exercise3.5.10
Wをブラウン運動,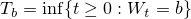 ,
, %7D.png) を前の記事と同じ確率測度とする.
を前の記事と同じ確率測度とする.%7D.png) を
を %7D.png) での期待値とすれば
での期待値とすれば
が成立する.
[証明]
あとは Exercise2.8.4 と同じように考えれば
λについての二次方程式 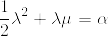 の解は
の解は 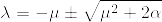 であり,
であり,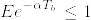 に注意してbの正負で場合分けしてλを選べば結論を得る.[証明終]
に注意してbの正負で場合分けしてλを選べば結論を得る.[証明終]
.png)
%3De%5E%7B-b%5Csqrt%7B2%5Calpha%7D%7D;%5Cquad%20b%3E0,%5Calpha%3E0.png)
.png)
)%3D0%5Cquad%20%7B%5Crm%20a.s.%7D.png)
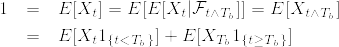
%3D1,%5Cquad%20%5Clim_%7Bt%5Cto%5Cinfty%7DX_t%3D0%5Cquad%20%7B%5Crm%20a.s.%7D,%5Cquad%20%20%7C1_%7B%5C%7Bt%3CT_b%5C%7D%7DX_t%7C%5Cleq%20e%5E%7B%5Clambda%20b%7D.png)
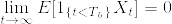
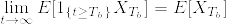
]%3D1.png)
]%3D1.png)
%7D(T%3C%5Cinfty)%3D1.png)
%5Cquad%20(%5Cmu%5Cneq%200).png)
%7D(A)%3DE[1_AZ_t];%5Cquad%20A%5Cin%20%5Cmathcal%7BF%7D_t%5EW.png)
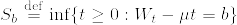
%7D[T%5Cleq%20t]%5Cquad%20(0%5Cleq%20t%3C%5Cinfty)%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DZ_t]%20%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DE[Z_t%7C%5Cmathcal%7BF%7D_%7Bt%5Cwedge%20T%7D]]%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DZ_%7Bt%5Cwedge%20T%7D]%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DZ_T].png)
%7D(T%3C%5Cinfty)%3DE[Z_T]%3DE[%5Cexp%20(%5Cmu%20W_T-%5Cfrac%7B1%7D%7B2%7D%5Cmu%20%5E2%20T)].png)
%7D(S_b%3C%5Cinfty)%3DP%5E%7B(%5Cmu)%7D(%5Cinf%5C%7Bt%5Cgeq%200:%5Ctilde%7BW%7D_t%3Db%5C%7D)%3D1.png)
%7De%5E%7B-%5Calpha%20T_b%7D%3D%5Cexp%20(%5Cmu%20b-%7Cb%7C%5Csqrt%7B%5Cmu%5E2%20+2%5Calpha%7D).png)
%7D[%5Ctilde%7BX%7D_t]%5Cquad%20(0%5Cleq%20t%3C%5Cinfty)%5C%5C%0A%26%3D%26E%5E%7B(%5Cmu)%7D[E%5E%7B(%5Cmu)%7D[%5Ctilde%7BX%7D_t%7C%5Cmathcal%7BF%7D%5EW_%7Bt%5Cwedge%20T_b%7D]]%5C%5C%0A%26%3D%26E%5E%7B(%5Cmu)%7D[1_%7B%5C%7BT_b%3Et%5C%7D%7D%5Ctilde%7BX%7D_t]+E%5E%7B(%5Cmu)%7D[1_%7B%5C%7BT_b%5Cleq%20t%5C%7D%7D%5Ctilde%7BX%7D_%7BT_b%7D].png)
1_%7B%5C%7BT_b%3C%5Cinfty%5C%7D%7D]%3D1.png)