可分距離空間上のtightでない確率測度の例

完備可分距離空間上では確率測度の族 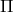がtightであることと，相対コンパクトであることは同値．けれども可分距離空間上の確率測度でtightでないものが存在する(よって相対コンパクトであるがtightでない例になっている)．

この例はBillingsleyの Convergence of Probability Measures の章末問題として載っていた例です．

Convergence of Probability Measures (Wiley Series in Probability and Statistics) (1999/07/30) Patrick Billingsley 商品詳細を見る

まず [0,1] の部分集合 S をルベーグ外測度が1，ルベーグ内測度が0であるようなルベーグ非可測集合とする(存在は認める)．この集合 S に [0,1] の相対位相を入れると，可分距離空間となる([0,1]の開基の元とSの共通部分から(あれば)一点とって集めた集合Aは可算集合でSで稠密)．またルベーグ外測度 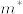を S に制限したものを 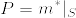とおく．Pは外測度の性質を満たし，カラテオドリの意味で可測な集合全体 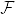の上の測度となる．また明らかに，任意のルベーグ可測集合 E に対して 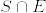は P可測集合である．さらにSのルベーグ外測度は1なので，PはSの上の確率測度となる．

ここで S の任意のコンパクト集合 K に対して P(K)=0 であることを示す(これよりPはtightでない S の上の確率測度となる)．包含写像 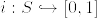は連続．よって i(K) は [0,1] のコンパクト集合．よって K は [0,1] のコンパクト集合．ここで 内測度の定義から

よって から ．以上より P は tight ではない．

Billingsleyはさらに可分距離空間上の確率測度の族で，相対コンパクトかつ各確率測度はtightだが，族はtightでないものも構成していて，証明できたらまたブログに書こうと思います．

しかし自分でもいろいろ考えてみたけど，ルベーグ非可測集合とは・・・