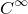cross variation の一意性(つづきのつづき)
cross variationの一意性はやはり言えることを,Doob-Meyer分解の証明(分解の一意性のところ)をみて思いました.
[証明]
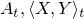 はどちらもnatural,increasingな過程の差で表されるから,任意の有界右連続マルチンゲール
はどちらもnatural,increasingな過程の差で表されるから,任意の有界右連続マルチンゲール 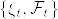 にたいして
にたいして
ただし,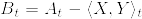 (有界変動)とした.また
(有界変動)とした.また 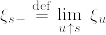 で左極限はほとんど確実なpathで存在する(*).[0,t]の任意の分割
で左極限はほとんど確実なpathで存在する(*).[0,t]の任意の分割 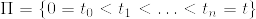 で
で
として,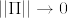 となるものを考える.
となるものを考える.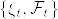 は有界であったから,ルベーグの優収束定理を(2回)用いれば
は有界であったから,ルベーグの優収束定理を(2回)用いれば
ところが
なので
よって 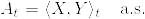 あとはpathの連続性からindistinguishabilityを除いてAと<X,Y>は等しい.[証明終]
あとはpathの連続性からindistinguishabilityを除いてAと<X,Y>は等しい.[証明終]
(*)の詳細はKaratzas-Shereveを参照してください.結局naturalという性質から一意性は出てくることがわかりました.2乗可積分連続マルチンゲールのときのcross variationの一意性ではまた別の証明がされていますが,連続単調増加関数はnaturalなので,上の議論からも一意性は出てくる気がします.わざわざ別証を付けるのは局所化の動機づけなのか,もしくは二次変分の性質を使いたかったからなのか,それとも上の証明が違うかのどれかだと思いました.
cross variation の一意性(つづき)
cross variation の一意性 で書いた証明は間違っていることに気づきました.<X>+2A+<Y>がincreasing であることを言うときにcross variation の全変動を抑える不等式は,間違えでした.
とりあえず調べてみるとIkeda-Watanabe(Stochastic Differential Equations and Diffusion Processes)のp53に証明があったので読んでみたのですが(以下その証明),これで一意性がいえていないのではないかと思います..
証明
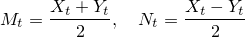 とし,M,Nの二次変分過程をそれぞれA,Bとする.このときXY-(A-B)はmartingaleになる.一意性はDoob-Meyer分解の一意性から従う.[証明終]
とし,M,Nの二次変分過程をそれぞれA,Bとする.このときXY-(A-B)はmartingaleになる.一意性はDoob-Meyer分解の一意性から従う.[証明終]
普通一意性を言うときはある上の条件を満たす過程Aがあって,実はA=<X,Y>ということを言わないといけないのではないかと思うのですが,上の証明でそれがいえているのかわからないです(というかいえていないのではないかと思います).もう少し考えてみて分かったらまた書こうと思います.
cross variation の一意性
主張
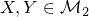 (2乗可積分マルチンゲールでかつ
(2乗可積分マルチンゲールでかつ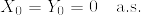 )とする.このとき
)とする.このとき_%7Bt%5Cgeq%200%7D.png) がマルチンゲールとなり,しかも
がマルチンゲールとなり,しかも %7D-A_t%5E%7B(2)%7D.png) という分解を持つものはindistinguishabilityを除いて一意である.ただし
という分解を持つものはindistinguishabilityを除いて一意である.ただし
とする.
証明
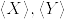 をX,Yの二次変分過程とする.
をX,Yの二次変分過程とする._%7Bt%5Cgeq%200%7D.png) がマルチンゲールであるから,
がマルチンゲールであるから,
もマルチンゲールである.Doob-Meyer分解の一意性(natural,increasingなので)より
より従う.
同様に
辺々引いて4で割れば
[証明終]
からしゅれの復習をしていてぱっと示せなかったので一応書き留めておくことにしました.連続だとさらに局所化のテクニックを使って連続なcross variationの一意性も示せます.この主張からcross variationの双線形性やシュワルツの不等式の類似物,cross variationの全変動を上から抑える不等式を得ることができ,Kunita-Watanabeの不等式などを得ることができるので,重要な主張だと思います.(Karatzas-Shreve参照)
確率積分における部分積分の公式
Problem3.3.12
とする.ただし,M,Nは連続局所マルチンゲール,B,Cは適合した連続で有界変動な過程とする.また 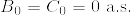 とする.このとき以下のような部分積分の公式が成立する.
とする.このとき以下のような部分積分の公式が成立する.
2つの式の片々引いて整理すると
を得る.[証明終]
pathが右(左)連続でadaptedならprogressively measurable
一度証明を書いておこうかと思います.
主張
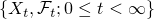 を実数に値を取る,右(左)連続で
を実数に値を取る,右(左)連続で .png) -adapted な過程とする.このとき過程Xは発展的可測である.
-adapted な過程とする.このとき過程Xは発展的可測である.
[証明]
右連続の場合のみ示す.左連続の場合も同様.%7D:%5COmega%5Ctimes%20[0,%5Cinfty)%5Crightarrow%20%5Cmathbf%7BR%7D.png) を以下のように定義する.
を以下のように定義する.
%7D.png) は
は 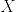 に各点収束する.実際
に各点収束する.実際 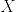 は右連続であるから任意の
は右連続であるから任意の 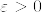 と任意の
と任意の .png) に対して,ある
に対して,ある 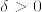 があって
があって
nを十分大にとれば,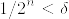 となるので,各点収束する.
となるので,各点収束する.%7D.png) は発展的可測であるから,各点収束先である
は発展的可測であるから,各点収束先である 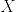 も発展的可測である.
も発展的可測である.
伊藤の公式は連続セミマルチンゲールの確率積分に対しての主張なので,発展的可測かどうか確かめる必要があるのですが,上の主張から問題ありませんでした.class DLの記事のときにもこの主張を確認したのですが,まだ馴染んでない気がしています.pathの片側連続性があれば,可測性には弱い仮定(adaptedだけ)仮定するだけで,発展的可測がでてくるのがしっくりきていない気がしています.
マルコフ過程で発展的可測であるが,強マルコフ過程でない例
からしゅれにも参照の本が挙げられていたけれど,ぐぐったら出てきたので紹介を.
The Strong Markov Property and Martingale Problems
この関数fを見つけてきたのはすごいと思いました.
ベクトル束に同伴する主ファイバー束の位相
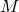 をn次元可微分多様体,
をn次元可微分多様体,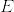 をr次元ベクトル束,
をr次元ベクトル束,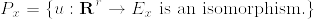 (
(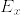 はファイバー)とし,
はファイバー)とし,
とする.また%5C%7D_%7B%5Calpha%5Cin%20A%7D.png) を局所座標近傍系,
を局所座標近傍系,.png) に対し
に対し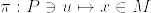 とする.
とする.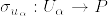 を局所的切断とする.つまり
を局所的切断とする.つまり 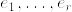 局所標構場とするとき,
局所標構場とするとき,)(%5Cmathbf%7Be%7D_j)%3De_j(x).png) (
(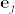 は標準基底)とする.ここで
は標準基底)とする.ここで
とすると,全単射となる.
Proposition1
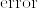 の部分集合
の部分集合 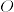 が開集合であることを,
が開集合であることを,
と定義する.開集合全体を 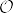 とすると,
とすると,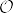 は開集合系の公理を満たす.
は開集合系の公理を満たす.
証明
任意のαに対して
証明
Mの任意の開集合Vと任意のαに対して
証明
位相の定義より明らか.[証明終]
Propositon4
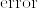 はハウスドルフ空間である.
はハウスドルフ空間である.
証明
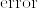 の相異なる二点
の相異なる二点 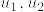 をとる.
をとる. %5Cneq%20%5Cpi(u_2).png) のときは多様体がハウスドルフ空間であることから,開集合で分離される.
のときは多様体がハウスドルフ空間であることから,開集合で分離される.%3D%20%5Cpi(u_2).png) のときは
のときは 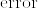 が同相で,
が同相で,%5Ctimes%20GL(r;%5Cmathbf%7BR%7D).png) がハウスドルフ空間であるから開集合で分離される.[証明終]
がハウスドルフ空間であるから開集合で分離される.[証明終]
は微分可能である.
証明
 とベクトル束の変換関数が微分可能であることから従う.[証明終]
とベクトル束の変換関数が微分可能であることから従う.[証明終]
]%3DE%5Cint_%7B(0,t]%7D%5Cxi_%7Bs-%7DdB_s.png)
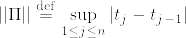
.png)
]%3D0%5Cquad%20(%7B%5Crm%20B%5C%20is%5C%20a%5C%20martingale.%7D).png)
]%3D0.png)
.png)
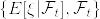
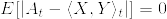
%7D:%7B%5Crm%20adapted,%5C%20natural,%5C%20increasing%5C%20process%5Cquad%20%7D(j%3D1,2).png)
%5E2-(%5Clangle%20X%5Crangle_t%20+%5Clangle%20Y%5Crangle_t%20+2A_t).png)
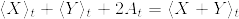
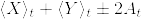
%5Cquad%20(%5Ccheck%7BA%7D_t:%7B%5Crm%20total%5C%20variation%5C%20of%7D%5C%20A%5C%20%7B%5Crm%20on%7D%5C%20[0,t]).png)
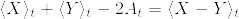
%3D%5Clangle%20X,Y%5Crangle_t.png)
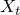
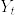
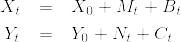
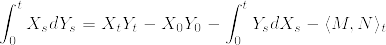
%7D_t%3DX_t+Y_t.png)
%3Dx%5E2/2.png)
%7D)%3Df(Z%5E%7B(1)%7D_0)+%5Cint_0%5Et(X_s+Y_s)dX_s+%5Cint_0%5Et(X_s+Y_s)dY_s+%5Cfrac%7B%5Clangle%20M+N%5Crangle_t%7D%7B2%7D.png)
%7D%3DX_t-Y_t.png)
%7D)%3Df(Z%5E%7B(2)%7D_0)+%5Cint_0%5Et(X_s-Y_s)dX_s-%5Cint_0%5Et(X_s-Y_s)dY_s+%5Cfrac%7B%5Clangle%20M-N%5Crangle_t%7D%7B2%7D.png)
%7D(%5Comega,t)%3DX(%5Comega,k/2%5En)%5C%20%7B%5Crm%20if%7D%5C%20t%5Cin%20[(k-1)/2%5En,k/2%5En)%5C%20%5C%20(k%3D1,2,%5Cdots).png)
,%5C%200%3Cu-t%3C%5Cdelta%20%5CRightarrow%20%7CX_u(%5Comega)-X_t(%5Comega)%7C%3C%5Cvarepsilon.png)

%5Cni%20%5Csigma_%7BU_%7B%5Calpha%7D%7D(x)%5Ccirc%20s%5Cmapsto%20(%5Cvarphi_%7B%5Calpha%7D(x),s)%5Cin%20%5Cvarphi_%7B%5Calpha%7D(U_%7B%5Calpha%7D)%5Ctimes%20GL(r;%5Cmathbf%7BR%7D).png)
)%20%7B%5C%20%5Crm%20is%5C%20open%5C%20in%5C%20%7D%20%5Cmathbf%7BR%7D%5En%5Ctimes%20GL(r;%5Cmathbf%7BR%7D)%5C%20%5Cforall%7B%5Calpha%7D%20.png)
)%3D%5Cvarphi_%7B%5Calpha%7D(U_%7B%5Calpha%7D)%5Ctimes%20GL(r;%5Cmathbf%7BR%7D).png)
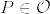
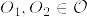
)%3D%5Ctilde%7B%5Cvarphi%7D_%7B%5Calpha%7D(O_1%5Ccap%20%5Cpi%5E%7B-1%7D(U_%7B%5Calpha%7D))%5Ccap%20%5Ctilde%7B%5Cvarphi%7D_%7B%5Calpha%7D(O_2%5Ccap%20%5Cpi%5E%7B-1%7D(U_%7B%5Calpha%7D)).png)
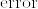
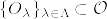
%5Cbigg)%3D%5Cbigcup_%7B%5Clambda%5Cin%5CLambda%7D%5Ctilde%7B%5Cvarphi%7D_%7B%5Calpha%7D(O_%7B%5Clambda%7D%5Ccap%20%5Cpi%5E%7B-1%7D(U_%7B%5Calpha%7D)).png)
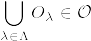
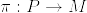
%5Ccap%20%5Cpi%5E%7B-1%7D(U_%7B%5Calpha%7D))%3D(V%5Ccap%20U_%7B%5Calpha%7D)%5Ctimes%20GL(r;%5Cmathbf%7BR%7D)%20.png)
%5Cin%5Cmathcal%7BO%7D.png)
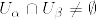
%5Ctimes%20GL(r;%5Cmathbf%7BR%7D)%5Crightarrow%20%5Cvarphi_%7B%5Calpha%7D(U_%7B%5Calpha%7D%5Ccap%20U_%7B%5Cbeta%7D)%5Ctimes%20GL(r;%5Cmathbf%7BR%7D).png)