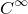ベクトル束に同伴する主ファイバー束の位相
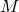 をn次元可微分多様体,
をn次元可微分多様体,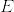 をr次元ベクトル束,
をr次元ベクトル束,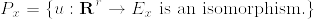 (
(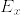 はファイバー)とし,
はファイバー)とし,
とする.また%5C%7D_%7B%5Calpha%5Cin%20A%7D.png) を局所座標近傍系,
を局所座標近傍系,.png) に対し
に対し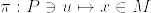 とする.
とする.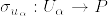 を局所的切断とする.つまり
を局所的切断とする.つまり 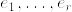 局所標構場とするとき,
局所標構場とするとき,)(%5Cmathbf%7Be%7D_j)%3De_j(x).png) (
(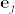 は標準基底)とする.ここで
は標準基底)とする.ここで
とすると,全単射となる.
Proposition1
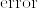 の部分集合
の部分集合 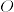 が開集合であることを,
が開集合であることを,
と定義する.開集合全体を 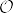 とすると,
とすると,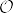 は開集合系の公理を満たす.
は開集合系の公理を満たす.
証明
任意のαに対して
証明
Mの任意の開集合Vと任意のαに対して
証明
位相の定義より明らか.[証明終]
Propositon4
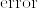 はハウスドルフ空間である.
はハウスドルフ空間である.
証明
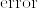 の相異なる二点
の相異なる二点 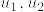 をとる.
をとる. %5Cneq%20%5Cpi(u_2).png) のときは多様体がハウスドルフ空間であることから,開集合で分離される.
のときは多様体がハウスドルフ空間であることから,開集合で分離される.%3D%20%5Cpi(u_2).png) のときは
のときは 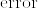 が同相で,
が同相で,%5Ctimes%20GL(r;%5Cmathbf%7BR%7D).png) がハウスドルフ空間であるから開集合で分離される.[証明終]
がハウスドルフ空間であるから開集合で分離される.[証明終]
は微分可能である.
証明
 とベクトル束の変換関数が微分可能であることから従う.[証明終]
とベクトル束の変換関数が微分可能であることから従う.[証明終]

%5Cni%20%5Csigma_%7BU_%7B%5Calpha%7D%7D(x)%5Ccirc%20s%5Cmapsto%20(%5Cvarphi_%7B%5Calpha%7D(x),s)%5Cin%20%5Cvarphi_%7B%5Calpha%7D(U_%7B%5Calpha%7D)%5Ctimes%20GL(r;%5Cmathbf%7BR%7D).png)
)%20%7B%5C%20%5Crm%20is%5C%20open%5C%20in%5C%20%7D%20%5Cmathbf%7BR%7D%5En%5Ctimes%20GL(r;%5Cmathbf%7BR%7D)%5C%20%5Cforall%7B%5Calpha%7D%20.png)
)%3D%5Cvarphi_%7B%5Calpha%7D(U_%7B%5Calpha%7D)%5Ctimes%20GL(r;%5Cmathbf%7BR%7D).png)
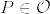
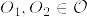
)%3D%5Ctilde%7B%5Cvarphi%7D_%7B%5Calpha%7D(O_1%5Ccap%20%5Cpi%5E%7B-1%7D(U_%7B%5Calpha%7D))%5Ccap%20%5Ctilde%7B%5Cvarphi%7D_%7B%5Calpha%7D(O_2%5Ccap%20%5Cpi%5E%7B-1%7D(U_%7B%5Calpha%7D)).png)
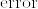
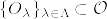
%5Cbigg)%3D%5Cbigcup_%7B%5Clambda%5Cin%5CLambda%7D%5Ctilde%7B%5Cvarphi%7D_%7B%5Calpha%7D(O_%7B%5Clambda%7D%5Ccap%20%5Cpi%5E%7B-1%7D(U_%7B%5Calpha%7D)).png)
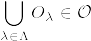
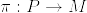
%5Ccap%20%5Cpi%5E%7B-1%7D(U_%7B%5Calpha%7D))%3D(V%5Ccap%20U_%7B%5Calpha%7D)%5Ctimes%20GL(r;%5Cmathbf%7BR%7D)%20.png)
%5Cin%5Cmathcal%7BO%7D.png)
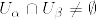
%5Ctimes%20GL(r;%5Cmathbf%7BR%7D)%5Crightarrow%20%5Cvarphi_%7B%5Calpha%7D(U_%7B%5Calpha%7D%5Ccap%20U_%7B%5Cbeta%7D)%5Ctimes%20GL(r;%5Cmathbf%7BR%7D).png)