モーメント母関数の条件付き期待値
次の記事でKaratzasAndShreveのProblem3.2.28の証明をしたいと思いますが,そこで使う補題を示しておこうと思います.
主張
.png) を確率空間とし,
を確率空間とし,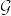 を
を 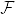 の部分σ加法族とする. また
の部分σ加法族とする. また 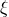 をほとんど確実に有界な
をほとんど確実に有界な 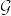 可測関数とし,
可測関数とし, 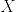 を平均 0 分散 t の正規分布に従う
を平均 0 分散 t の正規分布に従う 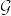 と独立な確率変数とする.このとき
と独立な確率変数とする.このとき
が成立する.つまり 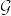 で条件付けると
で条件付けると 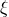 を定数と見なした
を定数と見なした 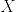 のモーメント母関数になっている.
のモーメント母関数になっている.
よって
となる.次に 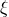 がほとんど確実に有界な一般の確率変数のときに示す.このとき単関数の列
がほとんど確実に有界な一般の確率変数のときに示す.このとき単関数の列 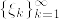 で
で
となるものが存在する.ここで
とすると,Vは可測である.さらに
であり,
である.よって条件付き期待値の優収束定理より
を得る.[証明終]
もっと簡単に示せそうな気もするんですが,とりあえず上のように愚直に示しました.あと細かい議論は抜きで条件付き期待値と可算和を交換しようとすると
途中で
であることを使いました.これでも期待値と和の交換の正当性が言えればいいと思います.
一様可積分かつ局所連続マルチンゲールであるがマルチンゲールでない例(M.Yor)
Exercise3.3.36
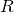 を0を出発するd(≧3)次元ベッセル過程とする.
を0を出発するd(≧3)次元ベッセル過程とする.;1%5Cleq%20t%3C%20%5Cinfty%5C%7D.png) は
は
(i) 局所マルチンゲールであり,
(ii) .png) に対して
に対して 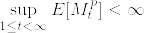 (従って一様可積分)を満たし,
(従って一様可積分)を満たし,
(iii) マルチンゲールでない
ことを示せ.
[証明]
(i)Rが有界な範囲で止めて伊藤の公式を用いると有界変動の項が消えるので局所連続マルチンゲールである.
(ii) Mは非負であるからフビニの定理より
ここで
となる.ただし半径rのd次元球の体積は %7D.png) であることを用いた.これより
であることを用いた.これより
を得る.
(iii) 背理法による.Mがマルチンゲールであるとする.(ii)より一様可積分であるから 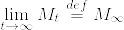 が存在して,かつ
が存在して,かつ  はマルチンゲールであり,
はマルチンゲールであり, 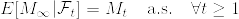 が成立する.ところがd≧3のとき
が成立する.ところがd≧3のとき 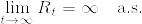 (KaratzasAndShreve,Problem3.3.24) なので
(KaratzasAndShreve,Problem3.3.24) なので 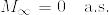 .従って
.従って
Levy's Characterization の反例っぽいもの(反例ではない)
Exercise3.3.17
%7D,W_t%5E%7B(2)%7D,W_t%5E%7B(3)%7D).png) を3次元の0を出発するブラウン運動とし,
を3次元の0を出発するブラウン運動とし,
とおく.このとき,どの二つのペア %7D,M%5E%7B(2)%7D),%5Cquad%20(M%5E%7B(1)%7D,M%5E%7B(3)%7D),%5Cquad%20(M%5E%7B(2)%7D,M%5E%7B(3)%7D).png) も2次元のブラウン運動になるが,
も2次元のブラウン運動になるが,%7D,M%5E%7B(2)%7D,M%5E%7B(3)%7D).png) は3次元のブラウン運動にならないことを示せ.またこれが,Levy's Characterization Theoremに矛盾しない理由を説明せよ.つまり,
は3次元のブラウン運動にならないことを示せ.またこれが,Levy's Characterization Theoremに矛盾しない理由を説明せよ.つまり,%7D,M%5E%7B(j)%7D%5Crangle_t%3D%5Cdelta_%7Bij%7Dt%5Cquad%20(i,j%3D1,2,3).png) で
で %7D%5Cquad%20(i%3D1,2,3).png) は局所連続マルチンゲールであるが,
は局所連続マルチンゲールであるが,%7D,M%5E%7B(2)%7D,M%5E%7B(3)%7D).png) は3次元のブラウン運動にならないのは矛盾でないのはなぜか.
は3次元のブラウン運動にならないのは矛盾でないのはなぜか.
[証明]
第1段
%7D_t.png) がブラウン運動であることを示す.そのために次の補題を用いる.(R.Durrett「Probability Theory and Examples」,4th-Edition,p302,303)
がブラウン運動であることを示す.そのために次の補題を用いる.(R.Durrett「Probability Theory and Examples」,4th-Edition,p302,303)
補題
 がブラウン運動であることと,以下の3条件を満たすことは同値である.
がブラウン運動であることと,以下の3条件を満たすことは同値である.
(i) はガウス過程である.
はガウス過程である.
(ii)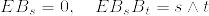
(iii) 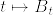 は確率1で連続.
は確率1で連続.
この補題より%7D_t.png) はブラウン運動である.実際(i)を満たすことは
はブラウン運動である.実際(i)を満たすことは .png) と
と %5Cquad%20(j%3D1,2,%5Cldots,n).png) に対して
に対して
上の式変形はXの値で分割して考えると得られる.また(ii)を満たすことは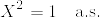 より従う.また(iii)は明らか.よってこの補題より
より従う.また(iii)は明らか.よってこの補題より%7D_t.png) はブラウン運動である.
はブラウン運動である.
第2段
%7D,M%5E%7B(2)%7D),%5Cquad%20(M%5E%7B(1)%7D,M%5E%7B(3)%7D),%5Cquad%20(M%5E%7B(2)%7D,M%5E%7B(3)%7D).png) が2次元のブラウン運動であることを示す.
が2次元のブラウン運動であることを示す. %7D,M%5E%7B(2)%7D).png) が2次元のブラウン運動であることは明らか.
が2次元のブラウン運動であることは明らか. %7D,M%5E%7B(3)%7D).png) が2次元のブラウン運動であることを示す.そのためには
が2次元のブラウン運動であることを示す.そのためには %7D_t-M%5E%7B(1)%7D_s.png) と
と %7D_t-M%5E%7B(3)%7D_s.png) が独立であることを示せばよい.それには任意のボレル集合A_1,A_2に対して
が独立であることを示せばよい.それには任意のボレル集合A_1,A_2に対して
が成立することを言えばよいが,それは上と同様にXの値で場合分けすれば示せる.同様にして %7D,M%5E%7B(3)%7D).png) も2次元のブラウン運動である.
も2次元のブラウン運動である.
第3段
%7D,M%5E%7B(2)%7D,M%5E%7B(3)%7D).png) が3次元のブラウン運動でないことを示す.背理法による.ブラウン運動であると仮定する.このとき
が3次元のブラウン運動でないことを示す.背理法による.ブラウン運動であると仮定する.このとき
よって
一方%7D,M%5E%7B(2)%7D,M%5E%7B(3)%7D).png) は0を出発するブラウン運動であるから,
は0を出発するブラウン運動であるから,%7D,M_1%5E%7B(2)%7D,M_1%5E%7B(3)%7D.png) は独立.したがって
は独立.したがって
よって(1),(2)式より
%7D,M%5E%7B(2)%7D,M%5E%7B(3)%7D).png) がブラウン運動であるとすると,
がブラウン運動であるとすると,
よって矛盾である.
第4段
Levy's Characterization Theoremに矛盾しない理由はフィルトレーションにある.つまり各過程が適合しているフィルトレーションに違いがあるので矛盾しない.[証明終]
長くなったので第4段についてはまた次の記事で書こうと思います.あとKaratzas&ShreveのBrownian Motion and Stochastic Calculusの本の問題は別のカテゴリ[KaratzasAndShreve]にすることにしました.
cross variation の一意性(つづきのつづき)
cross variationの一意性はやはり言えることを,Doob-Meyer分解の証明(分解の一意性のところ)をみて思いました.
[証明]
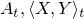 はどちらもnatural,increasingな過程の差で表されるから,任意の有界右連続マルチンゲール
はどちらもnatural,increasingな過程の差で表されるから,任意の有界右連続マルチンゲール 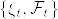 にたいして
にたいして
ただし,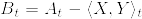 (有界変動)とした.また
(有界変動)とした.また 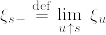 で左極限はほとんど確実なpathで存在する(*).[0,t]の任意の分割
で左極限はほとんど確実なpathで存在する(*).[0,t]の任意の分割 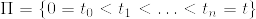 で
で
として,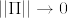 となるものを考える.
となるものを考える.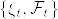 は有界であったから,ルベーグの優収束定理を(2回)用いれば
は有界であったから,ルベーグの優収束定理を(2回)用いれば
ところが
なので
よって 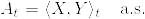 あとはpathの連続性からindistinguishabilityを除いてAと<X,Y>は等しい.[証明終]
あとはpathの連続性からindistinguishabilityを除いてAと<X,Y>は等しい.[証明終]
(*)の詳細はKaratzas-Shereveを参照してください.結局naturalという性質から一意性は出てくることがわかりました.2乗可積分連続マルチンゲールのときのcross variationの一意性ではまた別の証明がされていますが,連続単調増加関数はnaturalなので,上の議論からも一意性は出てくる気がします.わざわざ別証を付けるのは局所化の動機づけなのか,もしくは二次変分の性質を使いたかったからなのか,それとも上の証明が違うかのどれかだと思いました.
cross variation の一意性(つづき)
cross variation の一意性 で書いた証明は間違っていることに気づきました.<X>+2A+<Y>がincreasing であることを言うときにcross variation の全変動を抑える不等式は,間違えでした.
とりあえず調べてみるとIkeda-Watanabe(Stochastic Differential Equations and Diffusion Processes)のp53に証明があったので読んでみたのですが(以下その証明),これで一意性がいえていないのではないかと思います..
証明
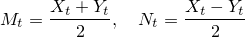 とし,M,Nの二次変分過程をそれぞれA,Bとする.このときXY-(A-B)はmartingaleになる.一意性はDoob-Meyer分解の一意性から従う.[証明終]
とし,M,Nの二次変分過程をそれぞれA,Bとする.このときXY-(A-B)はmartingaleになる.一意性はDoob-Meyer分解の一意性から従う.[証明終]
普通一意性を言うときはある上の条件を満たす過程Aがあって,実はA=<X,Y>ということを言わないといけないのではないかと思うのですが,上の証明でそれがいえているのかわからないです(というかいえていないのではないかと思います).もう少し考えてみて分かったらまた書こうと思います.
cross variation の一意性
主張
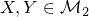 (2乗可積分マルチンゲールでかつ
(2乗可積分マルチンゲールでかつ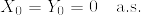 )とする.このとき
)とする.このとき_%7Bt%5Cgeq%200%7D.png) がマルチンゲールとなり,しかも
がマルチンゲールとなり,しかも %7D-A_t%5E%7B(2)%7D.png) という分解を持つものはindistinguishabilityを除いて一意である.ただし
という分解を持つものはindistinguishabilityを除いて一意である.ただし
とする.
証明
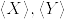 をX,Yの二次変分過程とする.
をX,Yの二次変分過程とする._%7Bt%5Cgeq%200%7D.png) がマルチンゲールであるから,
がマルチンゲールであるから,
もマルチンゲールである.Doob-Meyer分解の一意性(natural,increasingなので)より
より従う.
同様に
辺々引いて4で割れば
[証明終]
からしゅれの復習をしていてぱっと示せなかったので一応書き留めておくことにしました.連続だとさらに局所化のテクニックを使って連続なcross variationの一意性も示せます.この主張からcross variationの双線形性やシュワルツの不等式の類似物,cross variationの全変動を上から抑える不等式を得ることができ,Kunita-Watanabeの不等式などを得ることができるので,重要な主張だと思います.(Karatzas-Shreve参照)
確率積分における部分積分の公式
Problem3.3.12
とする.ただし,M,Nは連続局所マルチンゲール,B,Cは適合した連続で有界変動な過程とする.また 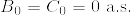 とする.このとき以下のような部分積分の公式が成立する.
とする.このとき以下のような部分積分の公式が成立する.
2つの式の片々引いて整理すると
を得る.[証明終]
%7C%5Cmathcal%7BG%7D]%3D%5Cexp%5Cbigg(%5Cfrac%7B1%7D%7B2%7D%5Cxi%5E2t%5Cbigg)%5Cquad%20%7B%5Crm%20a.s.%7D.png)
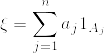
.png)
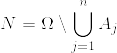
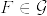
dP%26%3D%26%5Csum_%7Bj%3D1%7D%5En%5Cint_%7BF%5Ccap%20A_j%7D%5Cexp(a_jX)dP+P(F%5Ccap%20N)%5C%5C%0A%26%3D%26%20%5Csum_%7Bj%3D1%7D%5En%20%5Cexp%5Cbigg(%20%5Cfrac%7B1%7D%7B2%7Da_j%5E2t%5Cbigg)P(A_j%5Ccap%20F)+P(F%5Ccap%20N).png)
dP%3D%5Csum_%7Bj%3D1%7D%5En%5Cexp%5Cbigg(%5Cfrac%7B1%7D%7B2%7Da_j%5E2t%5Cbigg)P(A_j%5Ccap%20F)+P(F%5Ccap%20N).png)
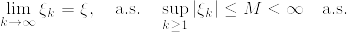
%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Cexp(M%7CX(%5Comega)%7C)+1.png)
%20X(%5Comega))%5Cleq%20V(%5Comega)%5Cquad%20%7B%5Crm%20a.s.%7D.png)
%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%20t%7D%7D%5Cexp(-%5Cfrac%7Bx%5E2%7D%7B2t%7D)dx+1%5C%5C%0A%26%5Cleq%262%5Cint_%7B%5Cmathbf%7BR%7D%7D%5Cexp(Mx)%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%20t%7D%7D%5Cexp(-%5Cfrac%7Bx%5E2%7D%7B2t%7D)dx%20+1%5C%5C%0A%26%3D%26%5Cexp%5Cbigg(%5Cfrac%7BM%5E2t%7D%7B2%7D%5Cbigg)%20+1%3C%5Cinfty.png)
%7C%5Cmathcal%7BG%7D]%26%3D%26%5Clim_%7Bn%5Cto%5Cinfty%7DE[%5Cexp(%5Cxi_n%20x)%7C%5Cmathcal%7BG%7D]%5C%5C%0A%26%3D%26%5Clim_%7Bn%5Cto%5Cinfty%7D%5Cexp%5Cbigg(%5Cfrac%7B1%7D%7B2%7D%5Cxi_n%5E2t%5Cbigg)%5C%5C%0A%26%3D%26%5Cexp%5Cbigg(%5Cfrac%7B1%7D%7B2%7D%5Cxi%5E2t%5Cbigg)%5Cquad%20%7B%5Crm%20a.s.%7D.png)
%7C%5Cmathcal%7BG%7D]%26%3D%26%5Csum_%7Bj%3D0%7D%5E%7B%5Cinfty%7D%5Cfrac%7B%5Cxi%5Ej%7D%7Bj!%7DE[X%5Ej%7C%5Cmathcal%7BG%7D]%5C%5C%0A%26%3D%26%5Csum_%7Bj%3D0%7D%5E%7B%5Cinfty%7D%5Cfrac%7B%5Cxi%5Ej%7D%7Bj!%7DE[X%5Ej]%5Cquad%20(%7B%5Crm%20independent%7D)%5C%5C%0A%26%3D%261+%5Csum_%7Bj%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B%5Cxi%5E%7B2j%7D%7D%7B(2j)!%7D%5Cfrac%7B(2j)!%7D%7B2%5Ejj!%7Dt%5E%7Bj%7D%5C%5C%0A%26%3D%261+%5Csum_%7Bj%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7Bj!%7D%5Cbigg(%5Cfrac%7B%5Cxi%5E2%20t%7D%7B2%7D%5Cbigg)%5Ej%5C%5C%0A%26%3D%26%5Cexp%5Cbigg(%5Cfrac%7B1%7D%7B2%7D%5Cxi%5E2t%5Cbigg).png)
!%7D%7B2%5Ejj!%7Dt%5Ej,%5Cquad%20E[X%5E%7B2j+1%7D]%3D0.png)
dy%5C%5C%0A%26%3D%26%5Cint_0%5E%7B1%7Dpy%5E%7Bp-1%7DP(M_t%3Ey)dy+%5Cint_1%5E%7B%5Cinfty%7Dpy%5E%7Bp-1%7DP(M_t%3Ey)dy%5C%5C%0A%26%5Cleq%26%5Cint_0%5E%7B1%7Dpy%5E%7Bp-1%7Ddy+%5Cint_1%5E%7B%5Cinfty%7Dpy%5E%7Bp-1%7DP(M_t%3Ey)dy%5C%5C%0A%26%3D%261+%5Cint_1%5E%7B%5Cinfty%7Dpy%5E%7Bp-1%7DP(M_t%3Ey)dy%5Cquad%20(p%3E0).png)
%26%3D%26%20P(R_t%5E2%3C%20r%5E2)%5Cquad%20(r%3D1/y%5E%7B1/d-2%7D)%5C%5C%0A%26%3D%26%5Cint_%7B%5C%7Bx_1%5E2+%5Cldots%20+x_d%5E2%3Cr%5E2%5C%7D%7D%5Cfrac%7B1%7D%7B(2%5Cpi%20t)%5E%7Bd/2%7D%7D%5Cexp(-%5Cfrac%7B%5Csum_%7Bj%3D1%7D%5Edx_j%5E2%7D%7B2t%7D)dx_1%5Cldots%20dx_d%5C%5C%0A%26%5Cleq%26%5Cfrac%7B1%7D%7B(2%5Cpi%20t)%5E%7Bd/2%7D%7D%5Cint_%7B%5C%7Bx_1%5E2+%5Cldots%20+x_d%5E2%3Cr%5E2%5C%7D%7Ddx_1%5Cldots%20dx_d%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B(2%5Cpi%20t)%5E%7Bd/2%7D%7D%20%5Cfrac%7B%5Cpi%5E%7Bd/2%7D%7D%7B%5CGamma(d/2+1)%7Dy%5E%7B-d/(d-2)%7D%0A.png)
%5E%7Bd/2%7D%7D%5Cfrac%7B%5Cpi%5E%7Bd/2%7D%7D%7B%5CGamma(d/2+1)%7D%5Cint_1%5E%7B%5Cinfty%7D%20y%5E%7Bp-1-d/(d-2)%7Ddy%5C%5C%0A%26%5Cleq%26%201+%5Cfrac%7B1%7D%7B(2t)%5E%7Bd/2%7D%5CGamma(d/2+1)(d/(d-2)-p)%7D%20.png)
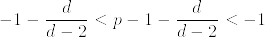
(d/(d-2)-p)%7D%20%3C%5Cinfty.png)
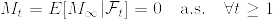
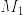
%3DP(R_1%5E2%5Cleq%201)%5Cgeq%20%5Cexp(-1/2)%5Cfrac%7B1%7D%7B2%5E%7Bd/2%7D%5CGamma(d/2+1)%7D%3E0.png)
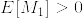
%7D).png)
%7D_t:%3DW_t%5E%7B(1)%7D,%5Cquad%20M_t%5E%7B(2)%7D:%3DW_t%5E%7B(2)%7D,%5Cquad%20M_t%5E%7B(3)%7D%3DXW_t%5E%7B(3)%7D.png)
%7D%5Cin%20A_%7Bt_1%7D,%5Cldots,M_%7Bt_n%7D%5E%7B(3)%7D%5Cin%20A_%7Bt_n%7D)%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B2%7DP(W_%7Bt_1%7D%5E%7B(3)%7D%5Cin%20A_%7Bt_1%7D,%5Cldots,W_%7Bt_n%7D%5E%7B(3)%7D%5Cin%20A_%7Bt_n%7D)+%5Cfrac%7B1%7D%7B2%7DP((-W_%7Bt_1%7D%5E%7B(3)%7D)%5Cin%20A_%7Bt_1%7D,%5Cldots,(-W_%7Bt_n%7D%5E%7B(3)%7D)%5Cin%20A_%7Bt_n%7D)%5C%5C%0A%26%3D%26P(W_%7Bt_1%7D%5E%7B(3)%7D%5Cin%20A_%7Bt_1%7D,%5Cldots,W_%7Bt_n%7D%5E%7B(3)%7D%5Cin%20A_%7Bt_n%7D).png)
%7D-M_s%5E%7B(1)%7D)%5Cin%20A_1,(M_t%5E%7B(3)%7D-M_s%5E%7B(3)%7D)%5Cin%20A_2)%5C%5C%0A%26%3D%26P((M_t%5E%7B(1)%7D-M_s%5E%7B(1)%7D)%5Cin%20A_1)P((M_t%5E%7B(3)%7D-M_s%5E%7B(3)%7D)%5Cin%20A_2).png)
%7DM_1%5E%7B(2)%7DM_1%5E%7B(3)%7D%3D%7CW_1%5E%7B(1)%7DW_1%5E%7B(2)%7DW_1%5E%7B(3)%7D%7C%5Cgeq%200.png)
%7DM_1%5E%7B(2)%7DM_1%5E%7B(3)%7D]%5Cgeq%200.png)
%7DM_1%5E%7B(2)%7DM_1%5E%7B(3)%7D]%3D%5Cprod_%7Bj%3D1%7D%5E3EM_1%5E%7B(j)%7D%3D0.png)
%7DM_1%5E%7B(2)%7DM_1%5E%7B(3)%7D%3D0%5Cquad%20%7B%5Crm%20a.s.%7D.png)
%7DM_1%5E%7B(2)%7DM_1%5E%7B(3)%7D%3D0)%5Cleq%20%5Csum_%7Bj%3D1%7D%5E3P(M_1%5E%7B(j)%7D%3D0)%3D0.png)
]%3DE%5Cint_%7B(0,t]%7D%5Cxi_%7Bs-%7DdB_s.png)
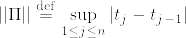
.png)
]%3D0%5Cquad%20(%7B%5Crm%20B%5C%20is%5C%20a%5C%20martingale.%7D).png)
]%3D0.png)
.png)
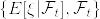
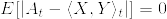
%7D:%7B%5Crm%20adapted,%5C%20natural,%5C%20increasing%5C%20process%5Cquad%20%7D(j%3D1,2).png)
%5E2-(%5Clangle%20X%5Crangle_t%20+%5Clangle%20Y%5Crangle_t%20+2A_t).png)
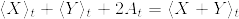
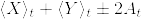
%5Cquad%20(%5Ccheck%7BA%7D_t:%7B%5Crm%20total%5C%20variation%5C%20of%7D%5C%20A%5C%20%7B%5Crm%20on%7D%5C%20[0,t]).png)
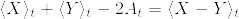
%3D%5Clangle%20X,Y%5Crangle_t.png)
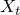
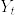
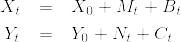
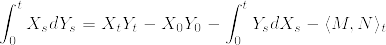
%7D_t%3DX_t+Y_t.png)
%3Dx%5E2/2.png)
%7D)%3Df(Z%5E%7B(1)%7D_0)+%5Cint_0%5Et(X_s+Y_s)dX_s+%5Cint_0%5Et(X_s+Y_s)dY_s+%5Cfrac%7B%5Clangle%20M+N%5Crangle_t%7D%7B2%7D.png)
%7D%3DX_t-Y_t.png)
%7D)%3Df(Z%5E%7B(2)%7D_0)+%5Cint_0%5Et(X_s-Y_s)dX_s-%5Cint_0%5Et(X_s-Y_s)dY_s+%5Cfrac%7B%5Clangle%20M-N%5Crangle_t%7D%7B2%7D.png)