Problem5.3.13
Problem5.3.13
%5Cquad%20((t,x)%5Cin[0,%5Cinfty)%5Ctimes%20%5Cmathbf%7BR%7D%5Ed).png) はd×d行列で,任意の(t,x)に対して正則であるとする.また
はd×d行列で,任意の(t,x)に対して正則であるとする.また %5Cquad%20((t,x)%5Cin%20[0,%5Cinfty)%5Ctimes%20%5Cmathbf%7BR%7D%5Ed).png) は一様に有界であり,
は一様に有界であり,%5Csigma(t,x)%5E%7B%5Ctop%7D.png) の最小固有値は(t,x)によらずに下から正の値で抑えられているとする.さらに
の最小固有値は(t,x)によらずに下から正の値で抑えられているとする.さらに
は初期分布 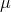 の弱解を持つとする.このとき確率微分方程式
の弱解を持つとする.このとき確率微分方程式
[証明]
まず %5E%7B-1%7Db(t,x)%5Cparallel%5E2%5Cquad%20(%5Cparallel%5Ccdot%5Cparallel:%7B%5Crm%20Euclidean%5C%20norm%7D).png) が(t,x)によらずに一様に上から抑えられることを示す.
が(t,x)によらずに一様に上から抑えられることを示す. %5Csigma(t,x)%5E%7B%5Ctop%7D.png) の固有ベクトルを正規直交基底として選び
の固有ベクトルを正規直交基底として選び ,a_2(t,x),%5Cldots,a_d(t,x).png) とし ,対応する固有値を
とし ,対応する固有値を %5Cleq%5Cldots%5Cleq%20%5Clambda_d(t,x).png) とする.ただしλは(t,x)によらない正の定数である.このとき,
とする.ただしλは(t,x)によらない正の定数である.このとき,
となるから
これより
これよりNovikovの条件からGirsanovの定理を用いて
は .png) の下でブラウン運動となる.よって
の下でブラウン運動となる.よって
(※)の等号は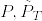 -a.s.で成立します.考えている確率空間が違いますが成立します(Karatzas and Shreve Problem3.5.6)
-a.s.で成立します.考えている確率空間が違いますが成立します(Karatzas and Shreve Problem3.5.6)
Exercise3.5.11(Robins&Siegmund(1973))
Exercise3.5.11
ν>0, c>1 に対して次のような 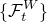 -stopping time を定義する.
-stopping time を定義する.
このとき
[証明]
より
あとは %7DR_c%3C%5Cinfty.png) であることを示せば十分である.なぜならばこれが成立すればWaldの恒等式から
であることを示せば十分である.なぜならばこれが成立すればWaldの恒等式から
となり,(1)の両辺の期待値をとって整理すれば
を得るからである.実際計算してみると
となり,証明が終わる.[証明終]
最後のR_cの可積分性を示すのに苦労しました.
Exercise3.5.10
Exercise3.5.10
Wをブラウン運動,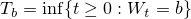 ,
, %7D.png) を前の記事と同じ確率測度とする.
を前の記事と同じ確率測度とする.%7D.png) を
を %7D.png) での期待値とすれば
での期待値とすれば
が成立する.
[証明]
あとは Exercise2.8.4 と同じように考えれば
λについての二次方程式 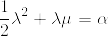 の解は
の解は 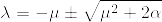 であり,
であり,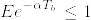 に注意してbの正負で場合分けしてλを選べば結論を得る.[証明終]
に注意してbの正負で場合分けしてλを選べば結論を得る.[証明終]
Problem3.5.7
Problem3.5.7
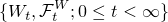 を一次元のブラウン運動とする.ただしフィルとレーションはWを可測にする最小のσ加法族とする.Tを
を一次元のブラウン運動とする.ただしフィルとレーションはWを可測にする最小のσ加法族とする.Tを.png) -stopping time でかつ,
-stopping time でかつ,%3D1.png) を満たすものとする.このときWaldの恒等式
を満たすものとする.このときWaldの恒等式
が成立することと,
として定義したものを 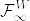 に一意的に拡張した測度である(Karatzas and Shreve, Corollary 3.5.2参照).
に一意的に拡張した測度である(Karatzas and Shreve, Corollary 3.5.2参照).
は上の条件を満たす.(Novikov conditionの証明に用いられる(Proposition 3.5.12))
[証明]
Optional Sampling Theoremから
よって単調収束定理から
特に, なら
なら  なので
なので %5Cleq%20P(S_b%3C%5Cinfty)%3D1.png) で
で %7D.png) のもとで,
のもとで,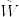 はブラウン運動になる(Girsanovの定理)ので
はブラウン運動になる(Girsanovの定理)ので
[証明終]
Xを時間に関して一様でないマルコフ過程とするとき,(t,X_t)は時間に関して一様なマルコフ過程となる.
ChapterIII Exercise(1.11) (Revuz-Yor)
Xが時間に関して一様でないE値マルコフ過程とするとき,(t,X_t)は時間に関して一様なR_+×E値マルコフ過程となる(これを"time-space" processと呼ぶ)ことを示せ. またこのとき,推移関数(transition function)を書き下せ.
[証明]
Xは時間に関して一様でないマルコフ過程なので,あるフィルター付き確率空間 ,Q).png) で Xは
で Xは .png) に適合し,任意の有界な非負値可測関数 f,
に適合し,任意の有界な非負値可測関数 f, 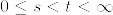 , 推移関数
, 推移関数 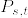 で
で
が成立している.初期測度を 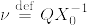 とする.Thorem(1,4)[Revuz-Yor, p81]より,任意の
とする.Thorem(1,4)[Revuz-Yor, p81]より,任意の 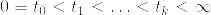 と非負値有界可測関数 f_i に対して
と非負値有界可測関数 f_i に対して
が成立している.ここで %5Cotimes%20%5Cmathcal%7BE%7D).png) 上の確率測度を次のように定義する.
上の確率測度を次のように定義する.%5Cin%20%5Cmathbf%7BR%7D_+%5Ctimes%20E,%5Cquad%20A%5Ctimes%20B%5Cin%20%5Cmathcal%7BB%7D(%5Cmathbf%7BR%7D_+)%5Ctimes%20%5Cmathcal%7BE%7D.png) に対して
に対して
つまり, ,%5Ccdot)%3D%5Cdelta_%7Bu+t-s%7D%5Cotimes%20P_%7Bu,u+t-s%7D(x,%5Ccdot).png) とする.このとき,R_{t,s} は時間に関して一様である.つまり,
とする.このとき,R_{t,s} は時間に関して一様である.つまり,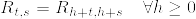 が成立する.
が成立する. 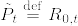 とすると,Fubiniの定理より
とすると,Fubiniの定理より 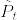 は推移関数となる.また 任意の
は推移関数となる.また 任意の 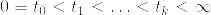 と非負値有界可測関数 f_i, g_i に対して
と非負値有界可測関数 f_i, g_i に対して
となることもFubiniの定理から分かる.%5Cotimes%20%5Cmathcal%7BE%7D.png) 可測関数を単関数近似して,一般の有界非負値可測関数について上と同じ等式を得るので,再びThorem(1,4)[Revuz-Yor, p81]より(t,X_t)は時間に関して一様なマルコフ過程となる.[証明終]
可測関数を単関数近似して,一般の有界非負値可測関数について上と同じ等式を得るので,再びThorem(1,4)[Revuz-Yor, p81]より(t,X_t)は時間に関して一様なマルコフ過程となる.[証明終]
少し混乱してR_{s,t}を定義するのに苦労しました.
LCH,second countableな空間の点を分離する非負値C_0関数列
主張
Eを局所コンパクトハウスドルフ(以下LCHと略す)かつ第2可算公理を満たす空間とし,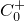 をE上の非負値連続関数で無限遠点で消える関数全体とする.このとき関数列
をE上の非負値連続関数で無限遠点で消える関数全体とする.このとき関数列 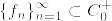 で任意の相異なるEの2点x,yに対してあるf_nがあってf_n(x)≠f_n(y)となるものが存在する.
で任意の相異なるEの2点x,yに対してあるf_nがあってf_n(x)≠f_n(y)となるものが存在する.
補題
Eが主張の条件を満たすとき,Eの任意の開集合Oはσコンパクトである.
[補題の証明]
次の事実を用いる.
事実
XがLCHであり,K⊂U⊂XでKはコンパクト,Uは開集合であるとき,相対コンパクトな開集合Vが存在して 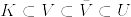 となる.(Folland, 猪狩参照)
となる.(Folland, 猪狩参照)
これから任意のx∈Oに対してある開近傍V_xが存在して 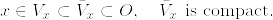 となる.
となる.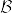 をEの可算開基とすると,
をEの可算開基とすると,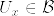 で
で  となるものが存在する.従って
となるものが存在する.従って 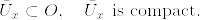 となる.以上より
となる.以上より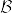 は可算であるから,Oはσコンパクトである.[補題証明終]
は可算であるから,Oはσコンパクトである.[補題証明終]
[主張の証明]
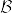 をEの可算開基とし,
をEの可算開基とし,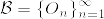 とする.各O_nは上の補題からσコンパクトであるから
とする.各O_nは上の補題からσコンパクトであるから
となるものが存在する.%7D%5C%7D_%7Bj,n%5Cin%20%5Cmathbf%7BN%7D%7D.png) が主張にある関数列の条件を満たすことはEがハウスドルフで,開基の元で2点を分離できることから明らか.[証明終]
が主張にある関数列の条件を満たすことはEがハウスドルフで,開基の元で2点を分離できることから明らか.[証明終]
Yorの本だと証明のなかでこれを使うのですが,主張だけ書いてあって証明はなかったので自分で付けてみました.少し回りくどい気もします.
dW_t;%5Cquad%200%5Cleq%20t%5Cleq%20T%5Cquad%20(W:%7B%5Crm%20Brownian%5C%20motion%7D).png)
dt+%5Csigma(t,X_t)dW_t.png)
%3D%5Csum_%7Bj%3D1%7D%5Enc_j(t,x)a_j(t,x),%5Cquad%20%5Cparallel%20b(t,x)%5Cparallel%5E2%3D%5Csum_%7Bj%3D1%7D%5En%7Cc_j(t,x)%7C%5E2.png)
%5E%7B-1%7Db(t,x)%5Cparallel%5E2%5C%5C%0A%26%3D%26b(t,x)%5E%7B%5Ctop%7D(%5Csigma(t,x)%5Csigma(t,x)%5E%7B%5Ctop%7D)%5E%7B-1%7Db(t,x)%5C%5C%0A%26%3D%26%5Csum_%7Bi%3D1%7D%5En%5Csum_%7Bj%3D1%7D%5Enc_i(t,x)c_j(t,x)a_i(t,x)(%5Csigma(t,x)%5Csigma(t,x)%5E%7B%5Ctop%7D)%5E%7B-1%7Da_j(t,x)%5C%5C%0A%26%3D%26%5Csum_%7Bi%3D1%7D%5En%5Csum_%7Bj%3D1%7D%5En%5Cfrac%7Bc_i(t,x)c_j(t,x)%7D%7B%5Clambda_j(t,x)%7Da_i(t,x)a_j(t,x)%5C%5C%0A%26%3D%26%5Csum_%7Bi%3D1%7D%5En%5Cfrac%7Bc_i(t,x)%5E2%7D%7B%5Clambda_i(t,x)%7D%5Cquad%20(%5C%7Ba_i(t,x)%5C%7D:%7B%5Crm%20orthonormal%5C%20basis%7D)%5C%5C%0A%26%5Cleq%20%26%5Cfrac%7B1%7D%7B%5Clambda%7D%5Cparallel%20b(t,x)%5Cparallel%5E2%5C%5C%0A%26%5Cleq%20%26M%5Cquad%20(M:%7B%5Crm%20const%7D,%5Cquad%20b(t,x):%7B%5Crm%20uniformly%5C%20bounded%7D).png)
,(%5COmega,%5Cmathcal%7BF%7D,P),%5C%7B%5Cmathcal%7BF%7D_t%5C%7D.png)
%5E%7B-1%7Db(s,X_s)%5Cparallel%5E2ds%5Cbigg)%5Cbigg]%26%5Cleq%26%5Cexp(Mt/2)%5C%5C%0A%26%3C%26%5Cinfty%20%5Cquad%20(0%5Cleq%20t%3C%5Cinfty).png)
%5E%7B-1%7Db(s,X_s)ds%5Cquad%20(0%5Cleq%20t%5Cleq%20T).png)
dW_s%3D%5Cint_0%5Etb(s,X_s)ds+%5Cint_0%5Et%5Csigma(s,X_s)d%5Ctilde%7BW%7D_s.png)
,(%5COmega,%5Cmathcal%7BF%7D_T,%5Ctilde%7BP%7D_T),%5C%7B%5Cmathcal%7BF%7D_t%5C%7D.png)
%3Dc%5C%7D.png)
%7DR_c%3D%5Cfrac%7B2%5Clog%20c%7D%7B%5Cnu%5E2%7D..png)
)%5C%5C%0A%26%3D%26%5Clim_%7Bt%5Cto%5Cinfty%7DE[1_%7B%5C%7BR_c%5Cleq%20t%5C%7D%7DZ_%7BR_c%7D]%5Cquad%20(%7B%5Crm%20by%5C%20the%5C%20monotone%5C%20convergence%5C%20thoerem%7D)%5C%5C%0A%26%3D%26%5Clim_%7Bt%5Cto%5Cinfty%7DE[1_%7B%5C%7BR_c%5Cleq%20t%5C%7D%7DZ_%7BR_c%5Cwedge%20t%7D]%5C%5C%0A%26%3D%26%5Clim_%7Bt%5Cto%5Cinfty%7DE[1_%7B%5C%7BR_c%5Cleq%20t%5C%7D%7DE[Z_t%7C%5Cmathcal%7BF%7D_%7Bt%5Cwedge%20R_c%7D]]%5Cquad%20(%7B%5Crm%20by%5C%20the%5C%20optional%5C%20sampling%5C%20theorem%7D)%5C%5C%0A%26%3D%26%5Clim_%7Bt%5Cto%5Cinfty%7DE[E[1_%7B%5C%7BR_c%5Cleq%20t%5C%7D%7DZ_t%7C%5Cmathcal%7BF%7D_%7Bt%5Cwedge%20R_c%7D]]%5C%5C%0A%26%3D%26%5Clim_%7Bt%5Cto%5Cinfty%7DE[1_%7B%5C%7BR_c%5Cleq%20t%5C%7D%7DZ_t]%5C%5C%0A%26%3D%26%5Clim_%7Bt%5Cto%5Cinfty%7D(EZ_t-E[1_%7B%5C%7BR_c%3E%20t%5C%7D%7DZ_t])%5C%5C%0A%26%3D%261%5Cquad%20(%7B%5Crm%20by%5C%20the%5C%20Lebesgue%5C%20convergence%5C%20theorem%7D).png)
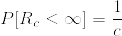
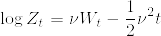
.png)
%7DW_%7BR_c%7D%3DE%5E%7B(%5Cnu)%7D%5Ctilde%7BW%7D_%7BR_c%7D+%5Cnu%20E%5E%7B(%5Cnu)%7DR_c%3D%5Cnu%20E%5E%7B(%5Cnu)%7DR_c.png)
%7DR_c%3D%5Cfrac%7B2%5Clog%20c%7D%7B%5Cnu%5E2%7D.png)
%7DR_c%26%3D%26%5Cint_0%5E%7B%5Cinfty%7DP%5E%7B(%5Cnu)%7D[R_c%5Cgeq%20t]dt%5C%5C%0A%26%5Cleq%26%5Cint_0%5E%7B(4%5Clog%20c)/%5Cnu%5E2%7DP%5E%7B(%5Cnu)%7D[R_c%5Cgeq%20t]dt+%5Cint_%7B(4%5Clog%20c)/%5Cnu%5E2%7D%5E%7B%5Cinfty%7DP%5E%7B(%5Cnu)%7D[R_c%5Cgeq%20t]dt%5C%5C%0A%26%5Cleq%20%26(4%5Clog%20c)/%5Cnu%5E2+%5Cint_%7B(4%5Clog%20c)/%5Cnu%5E2%7D%5E%7B%5Cinfty%7DP%5E%7B(%5Cnu)%7D[%5Ctilde%7BW%7D_t%5Cleq%20-%5Cnu%20t/4]dt%5C%5C%0A%26%5Cleq%20%26(4%5Clog%20c)/%5Cnu%5E2%20+%20%5Cint_0%5E%7B%5Cinfty%7D%5Cbigg(%5Cint_%7B-%5Cinfty%7D%5E%7B-%5Cnu%20t/4%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%20t%7D%7D%5Cexp(-%5Cfrac%7Bx%5E2%7D%7B2t%7D)%5Cbigg)dt%5C%5C%0A%26%3D%26(4%5Clog%20c)/%5Cnu%5E2%20+%20%5Cint_0%5E%7B%5Cinfty%7D%5Cbigg(%5Cint_%7B%5Cnu%20%5Csqrt%7Bt%7D/4%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%7D%5Cexp(-%5Cfrac%7Bu%5E2%7D%7B2%7D)%5Cbigg)dt%5C%5C%0A%26%5Cleq%20%26(4%5Clog%20c)/%5Cnu%5E2%20+%20%5Cint_0%5E%7B%5Cinfty%7D%5Cfrac%7B4%7D%7B%5Cnu%5Csqrt%7Bt%7D%7D%5Cexp(-%5Cnu%5E2t/32)dt%5C%5C%0A%26%3D%26(4%5Clog%20c)/%5Cnu%5E2%20+%5Cfrac%7B4%7D%7B%5Cnu%7D%5CGamma(3/2)(%5Cnu%5E2/32)%5E%7B-3/2%7D%3C%5Cinfty.png)
%7De%5E%7B-%5Calpha%20T_b%7D%3D%5Cexp%20(%5Cmu%20b-%7Cb%7C%5Csqrt%7B%5Cmu%5E2%20+2%5Calpha%7D).png)
%7D[%5Ctilde%7BX%7D_t]%5Cquad%20(0%5Cleq%20t%3C%5Cinfty)%5C%5C%0A%26%3D%26E%5E%7B(%5Cmu)%7D[E%5E%7B(%5Cmu)%7D[%5Ctilde%7BX%7D_t%7C%5Cmathcal%7BF%7D%5EW_%7Bt%5Cwedge%20T_b%7D]]%5C%5C%0A%26%3D%26E%5E%7B(%5Cmu)%7D[1_%7B%5C%7BT_b%3Et%5C%7D%7D%5Ctilde%7BX%7D_t]+E%5E%7B(%5Cmu)%7D[1_%7B%5C%7BT_b%5Cleq%20t%5C%7D%7D%5Ctilde%7BX%7D_%7BT_b%7D].png)
1_%7B%5C%7BT_b%3C%5Cinfty%5C%7D%7D]%3D1.png)
]%3D1.png)
%7D(T%3C%5Cinfty)%3D1.png)
%5Cquad%20(%5Cmu%5Cneq%200).png)
%7D(A)%3DE[1_AZ_t];%5Cquad%20A%5Cin%20%5Cmathcal%7BF%7D_t%5EW.png)
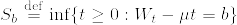
%7D[T%5Cleq%20t]%5Cquad%20(0%5Cleq%20t%3C%5Cinfty)%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DZ_t]%20%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DE[Z_t%7C%5Cmathcal%7BF%7D_%7Bt%5Cwedge%20T%7D]]%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DZ_%7Bt%5Cwedge%20T%7D]%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DZ_T].png)
%7D(T%3C%5Cinfty)%3DE[Z_T]%3DE[%5Cexp%20(%5Cmu%20W_T-%5Cfrac%7B1%7D%7B2%7D%5Cmu%20%5E2%20T)].png)
%7D(S_b%3C%5Cinfty)%3DP%5E%7B(%5Cmu)%7D(%5Cinf%5C%7Bt%5Cgeq%200:%5Ctilde%7BW%7D_t%3Db%5C%7D)%3D1.png)
.png)
%3De%5E%7B-b%5Csqrt%7B2%5Calpha%7D%7D;%5Cquad%20b%3E0,%5Calpha%3E0.png)
.png)
)%3D0%5Cquad%20%7B%5Crm%20a.s.%7D.png)
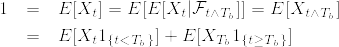
%3D1,%5Cquad%20%5Clim_%7Bt%5Cto%5Cinfty%7DX_t%3D0%5Cquad%20%7B%5Crm%20a.s.%7D,%5Cquad%20%20%7C1_%7B%5C%7Bt%3CT_b%5C%7D%7DX_t%7C%5Cleq%20e%5E%7B%5Clambda%20b%7D.png)
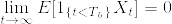
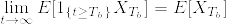
]%3D1.png)
%7C%5Cmathcal%7BG%7D_s]%3DP_%7Bs,t%7Df(X_s)%5Cquad%20%20Q%7B%5Crm%20-%5C%20a.s.%7D.png)
%5Cbigg]%5C%5C%0A%26%26%3D%5Cint_E%5Cnu(dx_0)f_0(x_0)%5Cint_EP_%7B0,t_1%7D(x_0,dx_1)f_1(x_1)%5Cldots%20%5Cint_EP_%7Bt_%7Bk-1%7D,t_k%7D(x_%7Bk-1%7D,dx_k)f_k(x_k).png)
,A%5Ctimes%20B)%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Cdelta_%7Bu+t-s%7D(A)P_%7Bu,u+t-s%7D(x,B)%5Cquad%20(%5Cdelta:%7B%5Crm%20Dirac%5C%20measure%7D).png)
g_i(X_%7Bt_i%7D)%5Cbigg]%3D%5C%5C%0A%26%26%5Cint_%7B%5Cmathbf%7BR%7D_+%5Ctimes%20E%7D%5Cdelta_0%5Cotimes%5Cnu%20(ds_0%5Cotimes%20dx_0)f_0(s_0)g_0(X_0)%5Cint_%7B%5Cmathbf%7BR%7D_+%5Ctimes%20E%7D%5Ctilde%7BP%7D_%7Bt_1%7D((s_0,x_0),dt_1%5Cotimes%20dx_1)f_1(s_1)g_1(X_%7Bt_1%7D)%5Cldots%20%5C%5C%0A%26%26%5Cint_E%5Ctilde%7BP%7D_%7Bt_k-t_%7Bk-1%7D%7D((s_%7Bk-1%7D,%20x_k),ds_k%5Cotimes%20dx_k)f_k(s_k)g_k(x_k).png)
%7D%5Cquad%20(K_j%5E%7B(n)%7D%20%7B%5Crm%5C%20is%5C%20compact%7D.).png)
%7D%5Cin%20C_0%5E+.png)
%7D(x)%3D1(%20x%5Cin%20K_j%5E%7B(n)%7D),%5Cquad%20%7B%5Crm%20supp%7Df_j%5E%7B(n)%7D%5Csubset%20O_n,%5Cquad%200%5Cleq%20f_j%5E%7B(n)%7D(x)%5Cleq%201%20(%5Cforall%7Bx%7D%5Cin%20E).png)