ゼータ分布に従う独立な確率変数が互いに素になる確率[D.Williams]
主張
X,Yは独立にゼータ分布に従うものとする.つまり
とする.このとき
(gcdは最大公約数)とすると,
となる.[D.Williams: Probability with martingales, p226]
証明
であるため.これより
となる.
次に.png) つまりX,Yが互いに疎になる確率を計算する.
つまりX,Yが互いに疎になる確率を計算する.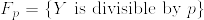 ,
,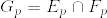 とすれば
とすれば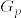 達は独立である.実際
達は独立である.実際
よりわかる.従って
\begin{eqnarray*}
P(H=1)
&=&P\bigg(\bigcap_{p:{\rm prime}}(E_p\cap F_p)^c\bigg)\\
&=&\prod_{p:{\rm prime}} P((E_p\cap F_p)^c)\\
&=&\prod_{p:{\rm prime}} (1-1/p^{2s})\\
&=&\frac{1}{\zeta(2s)}
\end{eqnarray*}
Xがpの倍数であるときのXの分布は,またゼータ分布になる:
nが素数でないときも
と定義すれば,条件付き期待値の性質から
となって示された.(包除原理を使って計算する方が正確だと思われます)[証明終]
ちなみにgcd(X,Y)の可測性は
から分かります.また結局互いに素な確率は
ということもわかり,面白いと思いました.
%3D%5Cfrac%7B1%7D%7Bn%5Es%5Czeta(s)%7D%20%5Cquad%20(%5Czeta(s):%3D%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7Bn%5Es%7D,s%3E1).png)
.png)
%3D%5Cfrac%7B1%7D%7Bn%5E%7B2s%7D%5Czeta(2s)%7D.png)
.png)
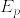
%26%3D%26%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7DP(X%3Dni_1%5Ccdots%20i_p)%5C%5C%0A%26%3D%26%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7B(ni_1%5Ccdots%20i_p)%5Es%5Czeta(s)%7D%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B(i_1%5Ccdots%20i_p)%5Es%7D.png)
%3D%5Cfrac%7B1%7D%7B(i_1%5Ccdots%20i_p)%5Es%7D.png)
%26%3D%26P(X%3D1)%5C%5C%0A%26%3D%26P%5Cbigg(%5Cbigcap_%7Bp:%7B%5Crm%20prime%7D%7DE_p%5Ec%5Cbigg)%5C%5C%0A%26%3D%26%5Cprod_%7Bp:%7B%5Crm%20prime%7D%7D(1-P(E_p))%5C%5C%0A%26%3D%26%5Cprod_%7Bp:%7B%5Crm%20prime%7D%7D(1-1/p%5Es).png)
%5C%5C%0A%26%3D%26P(E_%7Bi_1%7D%5Ccap%5Ccdots%20E_%7Bi_p%7D)P(F_%7Bi_1%7D%5Ccap%20%5Ccdots%20%5Ccap%20F_%7Bi_p%7D)%5Cquad%20(X,Y:%20%7B%5Crm%20independent%7D).png)
%3DP(X%3Dkp)/P(E_p)%3DP(X%3Dk).png)
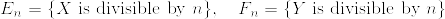
%26%3D%26P%5Cbigg(E_n%5Ccap%20F_n%5Ccap%20%5Cbigcap_%7Bp:%7B%5Crm%20prime%7D%7D(E_%7Bnp%7D%5Ccap%20F_%7Bnp%7D)%5Ec%20%5Cbigg)%5C%5C%0A%26%3D%26E%5Cbigg[1_%7BE_n%5Ccap%20F_n%7DP%5Cbigg(%5Cbigcap_%7Bp:%7B%5Crm%20prime%7D%7D(E_%7Bnp%7D%5Ccap%20F_%7Bnp%7D)%5Ec%7CE_n,F_n%5Cbigg)%5Cbigg]%5C%5C%0A%26%3D%26E[1_%7BE_n%7D1_%7BF_n%7DP(H%3D1)]%5C%5C%0A%26%3D%26n%5E%7B-2s%7D/%5Czeta(2s).png)
%3D%5Cprod_%7Bp:%7B%5Crm%20prime%7D%7D(p1_%7BE_p%7D1_%7BF_p%7D+%5Cmax%20%5C%7B1_%7BE_p%5Ec%7D,1_%7BF_p%5Ec%7D%5C%7D).png)
%3D1/%5Czeta(2s).png)