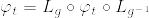fully T_4 ⇒ T_4
fully T_4 ⇒ T_4 の証明を思いついたのでメモ. (fully T_4 の定義は任意の開被覆に対して open star refinementが存在する.)
対遇をとって T_4 でない ⇒ fully T_4 でない ことを示す.
T_4でないとするとある互いに素な閉集合F_1,F_2があって,F_1,F_2を含む任意の開集合O_1⊃F_1, O_2⊃F_2に対して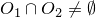 となる.開被覆
となる.開被覆 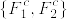 を考える.fully T_4であるとする.点xのopen star refinement を
を考える.fully T_4であるとする.点xのopen star refinement を 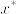 とする.このとき
とする.このとき
であるから仮定よりあるF_1の点a_1とF_2の点a_2があって
 の点aをとる.open star refinement の定義から
の点aをとる.open star refinement の定義から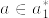 より
より 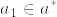 ,また
,また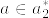 より
より 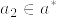 となるから
となるから 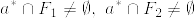 となる.ところが
となる.ところが 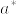 は
は 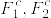 のいずれにも含まれないから矛盾.よってfully T_4ではない.
のいずれにも含まれないから矛盾.よってfully T_4ではない.
Scheffe's Lemma
David Williamsの『Probability with martingales』という本(下のやつ)のChapter5にあるScheffeの補題(5.10)のところにあるExerciseの証明のメモです.
 | Probability with Martingales (Cambridge Mathematical Textbooks) (1991/02/14) David Williams 商品詳細を見る |
まずFatouの補題より
また
より
a.s.収束と位相
Durrettの本に
Since there is a sequence of random variables that converges in probability but not a.s. , it follows that a.s. convergence does not come from a metric, or even from a topology.
とあった.
確率論の授業でも紹介されてた主張で,どう示すのかなと思っていたのだけれど,Durrettでは
Let 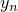 be a sequence of elements of a topological space. If every subsequence
be a sequence of elements of a topological space. If every subsequence %7D%0A.png) has a further subsequence
has a further subsequence %7D%0A.png) that converges to y then
that converges to y then  .
.
という主張から導けると書いてあった.
これからもしa.s.収束がある位相で定まると仮定して矛盾が導ける.確率収束する列から任意に部分列(確率収束する)をとって,Borel-Cantelliの補題からその確率収束先に概収束する部分列を取れる.概収束が位相から定まるという仮定と上の主張から,もとの確率収束する列は概収束する.これは矛盾.
という感じになる.
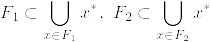
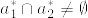
%3D%5Cbigg%5C%7B%20%5Comega:%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7B2%5En%7D%5Csup_%7B0%5Cleq%20t%5Cleq%20n%20,%20t%5Cin%20%5Cmathbf%7BQ%7D%7D(%7C%5Comega(t)-%5Comega_0(t)%7C%5Cwedge%201)%3C%5Cvarepsilon%5Cbigg%5C%7D.png)
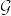
%5Cni%20%5Comega%20%5Cmapsto%20%5Comega(t)%5Cin%20%5Cmathbf%7BR%7D%20.png)
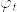
%5Cni%20%5Comega%20%5Cmapsto%20%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7B2%5En%7D%5Csup_%7B0%5Cleq%20t%5Cleq%20n,%20t%5Cin%5Cmathbf%7BQ%7D%7D(%7C%5Comega(t)-%5Comega_0(t)%7C%5Cwedge%201)%5Cin%20%5Cmathbf%7BR%7D.png)
%3D%5C%7B%5Cvarphi(%5Comega)%3C%5Cvarepsilon%5C%7D.png)
.png)
%5Cto%20%5Cmu(f%5E%7B%5Cpm%7D).png)
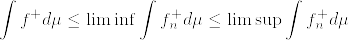
.png)
d%5Cmu%5C%5C%0A%26%5Cleq%20%26%20%5Climsup_n%20%5Cint%20(f_n%5E+-f%5E+)d%5Cmu+%5Climinf%5Cint%20(f_n%5E-%20-f%5E-)d%5Cmu%5C%5C%0A%26%5Cleq%20%26%20%5Climsup%5Cint%20%5C%7B(f_n%5E+-f%5E+)+(f_n%5E--f%5E-)%5C%7Dd%5Cmu%5C%5C%0A%26%5Cleq%20%26%20%5Climsup%5Cint%20%7Cf_n%7Cd%5Cmu%20-%5Cint%20%7Cf%7Cd%5Cmu%3D0.png)
%5Cto%20%5Cmu(f%5E%7B+%7D).png)
%5Cto%20%5Cmu(f%5E%7B-%7D).png)
%3D%5Csup%5C%7By%5Cin%5Cmathbf%7BR%7D:F(y)%5Cleq%5Comega%5C%7D.png)
%5Cleq%20a%5CLongleftrightarrow%20x%5Cleq%20Y(a).png)
%3E%20a%5CLongleftrightarrow%20x%3E%20Y(a).png)
.png)
%3CY(%5Comega).png)
)%5Cgeq%20F(Y(%5Comega_n))%5Cgeq%20%5Comega_n%20.png)
)%3C%20%5Comega.png)
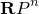
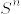

%5Ccong%20%5Cmathbf%7BR%7D.png)
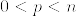
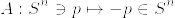
%3D%5C%7B%5Comega%20%5Cin%5COmega%5Ep(S%5En):A%5E*%5Comega%3D%5Comega%5C%7D.png)
%3D%5C%7B%5Cpi%5E*%5Calpha:%5Calpha%5Cin%5COmega%5Ep(%5Cmathbf%7BR%7DP%5En)%5C%7D.png)
%3D%5COmega_%7Bsym%7D%5Ep(S%5En).png)
.png)
%5C%20s.t.%5C%20%5Cpi%5E*%5Comega%20%3D%5Ceta.png)
%5Ccong%200.png)
%5C%20s.t.%5C%20d%5Cgamma%20%3D%5Ceta.png)
%5C%20s.t.%5C%20%5Cpi%5E*%5Cbeta%3D%5Cgamma.png)
%3Dd%5Cgamma%3D%5Ceta%3D%5Cpi%5E*%5Comega.png)
%3D%5Cpi%5E*%5Comega.png)
%5Clongrightarrow%20%5COmega_%7Bsym%7D%5Ep(S%5En).png)
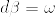
%5Ccong%200.png)
%5Ccong%20%5Cmathbf%7BR%7D%20%5CLongleftrightarrow%20M%20%7B%5Crm%5C%20is%5C%20orientable.%7D.png)
%5Ccong%20%5Cleft%0A%5C%7B%20%5Cbegin%7Barray%7D%7Bll%7D%0A%5Cmathbf%7BR%7D%20%26%20(n%5C%20%7B%5Crm%20:odd%7D)%5C%5C%20%0A0%20%26%20(n%5C%20%7B%5Crm%20:even%7D)%0A%5Cend%7Barray%7D%5Cright..png)
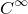
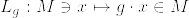
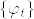
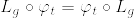
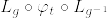
%5Ccirc%20(L_g%5Ccirc%20%5Cvarphi_%7Bs%7D%5Ccirc%20L_%7Bg%5E%7B-1%7D%7D).png)
)-f(g%5Ccdot%20g%5E%7B-1%7D%5Ccdot%20x)%7D%7Bt%7D.png)
(g%5E%7B-1%7D%5Ccdot%20x)%3D(L_g)_*X(f).png)