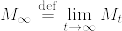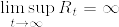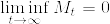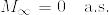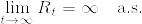LCH,second countableな空間の点を分離する非負値C_0関数列
主張
Eを局所コンパクトハウスドルフ(以下LCHと略す)かつ第2可算公理を満たす空間とし,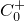 をE上の非負値連続関数で無限遠点で消える関数全体とする.このとき関数列
をE上の非負値連続関数で無限遠点で消える関数全体とする.このとき関数列 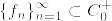 で任意の相異なるEの2点x,yに対してあるf_nがあってf_n(x)≠f_n(y)となるものが存在する.
で任意の相異なるEの2点x,yに対してあるf_nがあってf_n(x)≠f_n(y)となるものが存在する.
補題
Eが主張の条件を満たすとき,Eの任意の開集合Oはσコンパクトである.
[補題の証明]
次の事実を用いる.
事実
XがLCHであり,K⊂U⊂XでKはコンパクト,Uは開集合であるとき,相対コンパクトな開集合Vが存在して 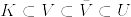 となる.(Folland, 猪狩参照)
となる.(Folland, 猪狩参照)
これから任意のx∈Oに対してある開近傍V_xが存在して 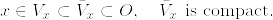 となる.
となる.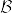 をEの可算開基とすると,
をEの可算開基とすると,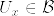 で
で  となるものが存在する.従って
となるものが存在する.従って 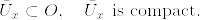 となる.以上より
となる.以上より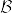 は可算であるから,Oはσコンパクトである.[補題証明終]
は可算であるから,Oはσコンパクトである.[補題証明終]
[主張の証明]
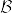 をEの可算開基とし,
をEの可算開基とし,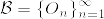 とする.各O_nは上の補題からσコンパクトであるから
とする.各O_nは上の補題からσコンパクトであるから
となるものが存在する.%7D%5C%7D_%7Bj,n%5Cin%20%5Cmathbf%7BN%7D%7D.png) が主張にある関数列の条件を満たすことはEがハウスドルフで,開基の元で2点を分離できることから明らか.[証明終]
が主張にある関数列の条件を満たすことはEがハウスドルフで,開基の元で2点を分離できることから明らか.[証明終]
Yorの本だと証明のなかでこれを使うのですが,主張だけ書いてあって証明はなかったので自分で付けてみました.少し回りくどい気もします.
正則+第2可算公理⇒正規
主張
正則(ハウスドルフ性を入れなくても良い)でかつ第2可算公理を満たす空間は,正規である.
[証明]
内田先生の集合と位相の本の演習問題(p107)になっていて,そこにある方針で示します.以下A,Bを互いに交わらない閉集合とする.
(1)開集合系{U_n}, {V_n}で
となり,さらに,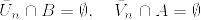 となるものが存在する.実際第2可算公理を満たすから可算開基を
となるものが存在する.実際第2可算公理を満たすから可算開基を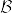 とすると,正則であることからAの任意の点xに対して,
とすると,正則であることからAの任意の点xに対して,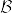 の元 U_x と 開集合 O_x で
の元 U_x と 開集合 O_x で
となる.同様にすればV_nも取れる.
(2) (1)の{U_n}, {V_n}に対して
とする.明らかにU,Vは開集合である.また .png) より
より 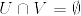 である.そして
である.そして
である.実際(1)より任意のx∈Aに対してあるNがあってx∈U_N. 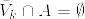 より,
より,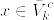 . よって x∈U'_n⊂U となる.B,Vの方も同様.[証明終]
. よって x∈U'_n⊂U となる.B,Vの方も同様.[証明終]
この主張から正則,第2可算公理,ハウスドルフを満たす空間は距離付け可能であることがわかります.
Exercise5.2.27
Exercise5.2.27
次の1次元確率微分方程式の解を陽に求めよ.
ただし,Wは1次元ブラウン運動とする.
[解]
%3D%5Csigma(x)%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Csqrt%7B1+x%5E2%7D.png) とすると,この確率微分方程式は
とすると,この確率微分方程式は
の解となる.σ(x)は2階連続微分可能で1階微分,2階微分ともにR上で有界である.b(x)も同様であるから,特にLipschitz連続である.従ってKaratzasShreve Proposition5.2.21より,次の常微分方程式を解くことで上の確率微分方程式の解を得ることができる.
ただし,
これを解いて
以上より解は
となる.[終]
ある種の確率微分方程式が常微分方程式を解くことで解を得ることができるという話題でした.上の場合f(x,y)がxによらないので楽でした.これがxによると常微分方程式を陽に解くことができないので,解析解は出ないように思います.
局所コンパクトハウスドルフ空間上では,ある連続関数の列でG-δコンパクト集合の定義関数に各点収束するものが存在する.
主張
局所コンパクトハウスドルフ(以下LCHとする)X上では,ある連続関数の列でG-δコンパクト集合Kの定義関数に各点収束するものが存在する.
[証明]
次の事実を用いる.
事実
LCHのコンパクト集合Kと開集合OでK⊂Oならば,コンパクト台をもつ実数値連続関数で 0≦u(x)≦1,u(x)=1 (x∈K),supp(u)⊂O となるものが存在する. (猪狩「実解析入門」6章などを参照)
.png) とする.上の事実から各nに対してコンパクト台をもつ連続関数の列
とする.上の事実から各nに対してコンパクト台をもつ連続関数の列 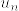 で
で
となるものが存在する.このとき
となる.実際任意のnで 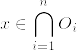 とすると,
とすると, 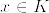 となり矛盾.このnにたいして,
となり矛盾.このnにたいして,%3D0.png)
さらにXが第二可算公理を満たすとコンパクトG_δ集合を含む最小のσ加法族はボレル集合族に一致します.
Exercise5.2.17(Ito-Watanabe(1978))
Problem3.3.23
Problem3.3.23
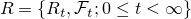 をd(≧3)次元のr(>0)を出発するベッセル過程とする.
をd(≧3)次元のr(>0)を出発するベッセル過程とする. 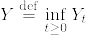 とするとき,
とするとき,
となることを示せ.つまりYはベータ分布に従う.
[証明]
伊藤の公式より,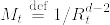 は局所連続マルチンゲールである.従ってあるstopping timeの列
は局所連続マルチンゲールである.従ってあるstopping timeの列 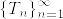 で
で %7D%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7DM_%7BT_n%5Cwedge%20t%7D.png) がマルチンゲールとなり,
がマルチンゲールとなり,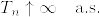 となるものが存在する.
となるものが存在する. %7D%5Cgeq%201/x%5E%7Bd-2%7D%5C%7D.png) ,
, 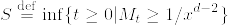 とすると,これらはstopping timeで,
とすると,これらはstopping timeで,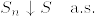 となる.
となる.
で, %7D1_%7B%5C%7BS_n%3D%5Cinfty%5C%7D%7D%7C%5Cleq%201/x%5E%7Bd-2%7D.png) ,
, %7D1_%7B%5C%7B0%3CS_n%3C%5Cinfty%5C%7D%7D%7C%3C1/x%5E%7Bd-2%7D.png) より条件付き期待値のルベーグの収束定理より,
より条件付き期待値のルベーグの収束定理より,
整理して
を得る.[証明終]
%7D%5Cquad%20(K_j%5E%7B(n)%7D%20%7B%5Crm%5C%20is%5C%20compact%7D.).png)
%7D%5Cin%20C_0%5E+.png)
%7D(x)%3D1(%20x%5Cin%20K_j%5E%7B(n)%7D),%5Cquad%20%7B%5Crm%20supp%7Df_j%5E%7B(n)%7D%5Csubset%20O_n,%5Cquad%200%5Cleq%20f_j%5E%7B(n)%7D(x)%5Cleq%201%20(%5Cforall%7Bx%7D%5Cin%20E).png)
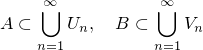
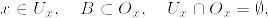
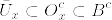
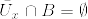
.png)
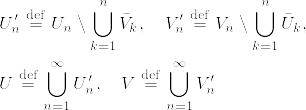

dt%20+%20%5Csqrt%7B1+X_t%5E2%7D%5C%20dW_t,%5Cquad%20P(X_0%3D%5Cxi)%3D1.png)
+%5Cfrac%7B1%7D%7B2%7D%5Csigma(X_s)%5Csigma'(X_s)%5Cbigg%5C%7Dds+%5Cint_0%5Et%5Csigma(X_s)dW_s.png)
,%5Cquad%20u(0,y)%3Dy..png)
%3Df(W_t(%5Comega),Y_t(%5Comega))%5Cquad%20%7B%5Crm%20with%7D%5Cquad%20Y_0(%5Comega)%3D%5Cxi(%5Comega).png)
%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Cfrac%7B1%7D%7B%5Crho%20(x,y)%7D,%5Cquad%20f(x,y)%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Crho(x,y)b(u(x,y))..png)
%3D%5Cfrac%7B1%7D%7B2%7D%5Cbigg%5C%7B(%5Csqrt%7B1+y%5E2%7D+y)e%5Ex-(%5Csqrt%7B1+y%5E2%7D-y)e%5E%7B-x%7D%5Cbigg%5C%7D.png)
%3D%5Csqrt%7B1+y%5E2%7D.png)
%3D%5Cfrac%7B1%7D%7B2%7D%5Cbigg%5C%7B(%5Csqrt%7B1+%5Cxi%5E2(%5Comega)%7D+%5Cxi(%5Comega))e%5Et-(%5Csqrt%7B1+%5Cxi%5E2(%5Comega)%7D-%5Cxi(%5Comega))e%5E%7B-t%7D%20%5Cbigg%5C%7D.png)
%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B2%7D%5Cbigg%5C%7B(%5Csqrt%7B1+Y_t%5E2%7D+Y_t)e%5E%7BW_t%7D-(%5Csqrt%7B1+Y_t%5E2%7D-Y_t)e%5E%7B-W_t%7D%20%5Cbigg%5C%7D%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B2%7D%5Cbigg%5C%7B(%5Csqrt%7B1+%5Cxi%5E2%7D+%5Cxi)e%5E%7Bt+W_t%7D%20-(%5Csqrt%7B1+%5Cxi%5E2%7D-%5Cxi)e%5E%7B-t-W_t%7D%5Cbigg%5C%7D.png)
%5Csubset%20%5Cbigcap_%7Bi%3D1%7D%5EnO_i,%5Cquad%20u_n(x)%3D1%5Cquad%20(x%5Cin%20K).png)
%3D%5Cleft%5C%7B%0A%5Cbegin%7Barray%7D%7Bll%7D%0A1%5Cquad%20(x%5Cin%20K)%5C%5C%0A0%5Cquad%20(x%5Cnot%5Cin%20K)%0A%5Cend%7Barray%7D%0A%5Cright..png)
%3D1%5Cquad%20(x%5Cin%20K).png)
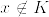
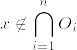
%3D0%5Cquad(x%5Cnot%20%5Cin%20K).png)
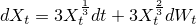
%7D%3D%5Cleft%5C%7B%0A%5Cbegin%7Barray%7D%7Bll%7D%0A0;%5Cquad%20%260%5Cleq%20t%3C%5Cbeta_%7B%5Ctheta%7D%5C%5C%0AW_t%5E3;%5Cquad%20%26%5Cbeta_%7B%5Ctheta%7D%5Cleq%20t%3C%5Cinfty%0A%5Cend%7Barray%7D%0A%5Cright..png)
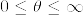
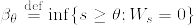
%7D.png)
%7D%3D0)%3D1.png)
%5E2%20%5C%7Dds%5Cbigg]%3D%5Cint_0%5EtE%5C%7B%20%7C3X_s%5E%7B%5Cfrac%7B1%7D%7B3%7D%7D%7C+(3X_s%5E%7B%5Cfrac%7B2%7D%7B3%7D%7D)%5E2%20%5C%7Dds%3C%5Cinfty%5Cquad%20(%5Cforall%7Bt%7D%5Cgeq%200,%20%7B%5Crm%20Fubini%7D).png)
%5E2%20%5C%7Dds%3C%5Cinfty%5Cbigg]%3D1.png)
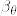
%7D%3D(W_t-W_%7Bt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D%7D)%5E3.png)
%7D%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7DW_t-W_%7Bt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D%7D.png)
%7D%3D(Z_t%5E%7B(%5Ctheta)%7D)%5E3%3D3%5Cint_0%5EtZ_s%5E%7B(%5Ctheta)%7Dd%5Clangle%20Z%5E%7B(%5Ctheta)%7D%5Crangle%20_s+3%5Cint_0%5Et(Z_s%5E%7B(%5Ctheta)%7D)%5E2dZ%5E%7B(%5Ctheta)%7D_s.png)
%7D_t%3D%5Cleft%5C%7B%0A%5Cbegin%7Barray%7D%7Bll%7D%0A0;%5Cquad%20%26(0%5Cleq%20t%3C%5Cbeta_%7B%5Ctheta%7D)%5C%5C%0AW_t;%5Cquad%20%26(%5Cbeta_%7B%5Ctheta%7D%5Cleq%20t%3C%5Cinfty)%0A%5Cend%7Barray%7D%0A%5Cright..png)
%7D%3D3%5Cint_0%5EtX_s%5E%7B(%5Ctheta)%7Dds+3%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E2dW_s.png)
%7D%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7DW_%7Bt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D%7D.png)
%7D)%5E%7B2/3%7DdZ_s%5E%7B(%5Ctheta)%7D%3D%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B2/3%7DdW_s-%5Cint_0%5Et%20(X_s%5E%7B(%5Ctheta)%7D)%5E%7B2/3%7DdA_s%5E%7B(%5Ctheta)%7D.png)
%7D)%5E%7B2/3%7DdA_s%5E%7B(%5Ctheta)%7D%5Cbigg)%5E2%5C%20%5Cbigg]%3DE%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B4/3%7Dd%5Clangle%20A%5E%7B(%5Ctheta)%7D%5Crangle_s.png)
%7D%5Crangle_t%3Dt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D.png)
%7D)%5E%7B4/3%7Dd%5Clangle%20A%5Crangle_s%5E%7B(%5Ctheta)%7D%5C%5C%0A%26%3D%26%5Cint_0%5E%7Bt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D%7D(X_s%5E%7B(%5Ctheta)%7D)%5E%7B4/3%7Dd%5Clangle%20A%5Crangle_s%5E%7B(%5Ctheta)%7D%3D0%5Cquad%20(X_t%5E%7B(%5Ctheta)%7D%3D0%5Cquad%200%5Cleq%20%5Cforall%7Bt%7D%5Cleq%20%5Cbeta_%7B%5Ctheta%7D).png)
%7D)%5E%7B1/3%7Dd%5Clangle%20Z%5E%7B(%5Ctheta)%7D_s%5C%5C%0A%26%3D%26%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B1/3%7Dds-2%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B1/3%7Dd%5Clangle%20W,A%5E%7B(%5Ctheta)%7D%5Crangle%20_s+%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B1/3%7Dd%5Clangle%20A%5E%7B(%5Ctheta)%7D%5Crangle_s.png)
%7D)%5E%7B1/3%7Dd%5Clangle%20A%5E%7B(%5Ctheta)%7D%5Crangle_s%3D0.png)
%7D)%5E%7B1/3%7Dd%5Clangle%20W,A%5E%7B(%5Ctheta)%7D%5Crangle%20_s%5Cbigg%7C%5Cleq%20%5Cbigg(%5Cint_0%5Et%20(X_s%5E%7B(%5Ctheta)%7D)%5E%7B2/3%7Dd%5Clangle%20A%5E%7B(%5Ctheta)%7D%5Crangle_s%5Cbigg)%5E%7B1/2%7D%5Cbigg(%5Cint_0%5Et1ds%5Cbigg)%5E%7B1/2%7D%3D0.png)
%3D%5Cbigg(%5Cfrac%7Bx%7D%7Br%7D%5Cbigg)%5E%7Bd-2%7D%5Cquad%20(0%5Cleq%20x%5Cleq%20r).png)
%7D%7C%5Cmathcal%7BF%7D_0]%3DM_%7B0%5Cwedge%20S_n%7D%5E%7B(n)%7D%3D1/r%5E%7Bd-2%7D%5Cquad%20%7B%5Crm%20a.s.%7D.png)
%7D%3DM_t%5E%7B(n)%7D1_%7B%5C%7BS_n%3D%5Cinfty%5C%7D%7D+M_%7Bt%5Cwedge%20S_n%7D%5E%7B(n)%7D1_%7B%5C%7B0%3CS_n%3C%5Cinfty%5C%7D%7D+M_0%5E%7B(n)%7D1_%7B%5C%7BS_n%3D0%5C%7D%7D.png)
%7D1_%7B%5C%7BS_n%3D%5Cinfty%5C%7D%7D%7C%5Cmathcal%7BF%7D_0]%3DE[M_%7BT_n%7D1_%7B%5C%7BS_n%3D%5Cinfty%5C%7D%7D%7C%5Cmathcal%7BF%7D_0].png)
%7D1_%7B%5C%7B0%3CS_n%3C%5Cinfty%5C%7D%7D%7C%5Cmathcal%7BF%7D_0]%3DE[M_%7BS_n%7D%5E%7B(n)%7D1_%7B%5C%7B0%3CS_n%3C%5Cinfty%5C%7D%7D%7C%5Cmathcal%7BF%7D_0].png)
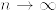
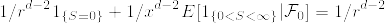
%3D1%5Cwedge%20(x/r)%5E%7Bd-2%7D.png)
%3D1.png)