ベクトル束に同伴する主ファイバー束の位相
 をn次元可微分多様体,
をn次元可微分多様体,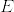 をr次元ベクトル束,
をr次元ベクトル束,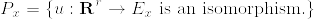 (
(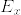 はファイバー)とし,
はファイバー)とし,
とする.また%5C%7D_%7B%5Calpha%5Cin%20A%7D.png) を局所座標近傍系,
を局所座標近傍系,.png) に対し
に対し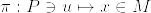 とする.
とする.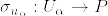 を局所的切断とする.つまり
を局所的切断とする.つまり 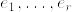 局所標構場とするとき,
局所標構場とするとき,)(%5Cmathbf%7Be%7D_j)%3De_j(x).png) (
( は標準基底)とする.ここで
は標準基底)とする.ここで
とすると,全単射となる.
Proposition1
 の部分集合
の部分集合  が開集合であることを,
が開集合であることを,
と定義する.開集合全体を  とすると,
とすると, は開集合系の公理を満たす.
は開集合系の公理を満たす.
証明
任意のαに対して
証明
Mの任意の開集合Vと任意のαに対して
証明
位相の定義より明らか.[証明終]
Propositon4
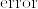 はハウスドルフ空間である.
はハウスドルフ空間である.
証明
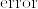 の相異なる二点
の相異なる二点 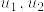 をとる.
をとる. %5Cneq%20%5Cpi(u_2).png) のときは多様体がハウスドルフ空間であることから,開集合で分離される.
のときは多様体がハウスドルフ空間であることから,開集合で分離される.%3D%20%5Cpi(u_2).png) のときは
のときは 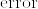 が同相で,
が同相で,%5Ctimes%20GL(r;%5Cmathbf%7BR%7D).png) がハウスドルフ空間であるから開集合で分離される.[証明終]
がハウスドルフ空間であるから開集合で分離される.[証明終]
は微分可能である.
証明
 とベクトル束の変換関数が微分可能であることから従う.[証明終]
とベクトル束の変換関数が微分可能であることから従う.[証明終]
多様体上の調和関数
Mをコンパクト,連結,向きづけられた境界付き可微分多様体とする.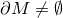 であるとする.M上の調和関数u,vが境界上で一致するときuとvはM上で一致する.
であるとする.M上の調和関数u,vが境界上で一致するときuとvはM上で一致する.
という主張の証明のメモ.
u-vを考えれば良いから,調和関数fで境界上で0となるものが,M上で恒等的に0になることを示せばよい. をMの体積要素とする.Stokesの定理から
をMの体積要素とする.Stokesの定理から
ただし境界にはMから定まる向きを入れ,Nは外向きの単位ベクトルとし,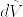 は境界の体積要素とする.fは調和で境界上で0となるから
は境界の体積要素とする.fは調和で境界上で0となるから
よって 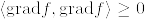 より
より 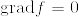 .ゆえにfは定数関数(任意のベクトル場Xに対してXf=0より).仮定より境界上で0で,Mは連結であったからf=0となる.
.ゆえにfは定数関数(任意のベクトル場Xに対してXf=0より).仮定より境界上で0で,Mは連結であったからf=0となる.
似たような主張で「Mの境界が空であったら調和関数は定数に限る(Mは向き付可能でなくても良い)」というのが松島多様体にあった.そちらもgrad fが0となることを示すために 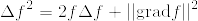 という式をつかい,ストークスの定理から導いていた.細かいけど
という式をつかい,ストークスの定理から導いていた.細かいけど  ではないだろうか.計算すると
ではないだろうか.計算すると
よって
となるから
となる気がするのだけど・・・
反例?
松島多様体で自明とあった補題.(前の記事参照→ Sardの定理 (続き) )
反例らしきものが出来たので.
まず多様体として  というものを考える.ただし
というものを考える.ただし 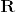 には通常の位相をいれ,
には通常の位相をいれ, 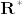 は
は 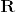 に離散位相を入れたものとし,多様体は直積位相をいれたものとする.
に離散位相を入れたものとし,多様体は直積位相をいれたものとする.
このとき  はHausdorff空間で(Hausdorff空間の直積はHausdorff空間になる),座標変換はRからRへの恒等写像のある開集合への制限であるから,これは1次元
はHausdorff空間で(Hausdorff空間の直積はHausdorff空間になる),座標変換はRからRへの恒等写像のある開集合への制限であるから,これは1次元 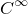 級多様体となる.
級多様体となる.
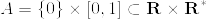 とすると,Aは
とすると,Aは  の測度0の集合であるが,
の測度0の集合であるが,%3D[0,1].png) でこれは測度0でない.よってこれが反例である.
でこれは測度0でない.よってこれが反例である.
なんか穴があるかもしれないけど,第二可算公理がないとやはりなんかダメな気がする.
臨界点
写像度の話を読んでいたら臨界点の集合が閉集合であることの証明を思いついたのでメモ.
M,Nを可微分多様体としそれぞれ次元をm,nとする.可微分写像f:M→Nとする.Mの正則点全体の集合が開集合であることを示せばよい.
m < nなら任意のMの点は臨界点であるから正則点全体は空集合であるから開である.
m >= nのとき.Mの任意の正則点xに対してxを含むあるMの座標近傍 ).png) とf(x)を含む
とf(x)を含む ).png) があって
があって
ただしDfは
.png)
を(i,j)成分にもつn×m行列である.rankがnなので _%7Bi,j%3D1,%5Ccdots,n%7D.png) が正則であるとしてよい.この行列式はR^mからRへの連続関数であるから
が正則であるとしてよい.この行列式はR^mからRへの連続関数であるから .png) の十分小さい近傍で0でない.つまりこの近傍上で
の十分小さい近傍で0でない.つまりこの近傍上で 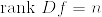 が成立している.これより正則点全体の集合をRとすれば,Rの任意の点は内点である.従ってRは開集合である.
が成立している.これより正則点全体の集合をRとすれば,Rの任意の点は内点である.従ってRは開集合である.

%5Cni%20%5Csigma_%7BU_%7B%5Calpha%7D%7D(x)%5Ccirc%20s%5Cmapsto%20(%5Cvarphi_%7B%5Calpha%7D(x),s)%5Cin%20%5Cvarphi_%7B%5Calpha%7D(U_%7B%5Calpha%7D)%5Ctimes%20GL(r;%5Cmathbf%7BR%7D).png)
)%20%7B%5C%20%5Crm%20is%5C%20open%5C%20in%5C%20%7D%20%5Cmathbf%7BR%7D%5En%5Ctimes%20GL(r;%5Cmathbf%7BR%7D)%5C%20%5Cforall%7B%5Calpha%7D%20.png)
)%3D%5Cvarphi_%7B%5Calpha%7D(U_%7B%5Calpha%7D)%5Ctimes%20GL(r;%5Cmathbf%7BR%7D).png)
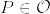
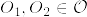
)%3D%5Ctilde%7B%5Cvarphi%7D_%7B%5Calpha%7D(O_1%5Ccap%20%5Cpi%5E%7B-1%7D(U_%7B%5Calpha%7D))%5Ccap%20%5Ctilde%7B%5Cvarphi%7D_%7B%5Calpha%7D(O_2%5Ccap%20%5Cpi%5E%7B-1%7D(U_%7B%5Calpha%7D)).png)
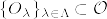
%5Cbigg)%3D%5Cbigcup_%7B%5Clambda%5Cin%5CLambda%7D%5Ctilde%7B%5Cvarphi%7D_%7B%5Calpha%7D(O_%7B%5Clambda%7D%5Ccap%20%5Cpi%5E%7B-1%7D(U_%7B%5Calpha%7D)).png)
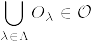
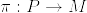
%5Ccap%20%5Cpi%5E%7B-1%7D(U_%7B%5Calpha%7D))%3D(V%5Ccap%20U_%7B%5Calpha%7D)%5Ctimes%20GL(r;%5Cmathbf%7BR%7D)%20.png)
%5Cin%5Cmathcal%7BO%7D.png)

%5Ctimes%20GL(r;%5Cmathbf%7BR%7D)%5Crightarrow%20%5Cvarphi_%7B%5Calpha%7D(U_%7B%5Calpha%7D%5Ccap%20U_%7B%5Cbeta%7D)%5Ctimes%20GL(r;%5Cmathbf%7BR%7D).png)
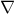

%5C%20(t_0,t%5Cin%20I).png)
%7DM.png)
%7DM.png)
.png)
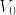
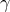
%3D%5Clim_%7Bt%5Cto%20t_0%7D%5Cfrac%7BP_%7Bt_0t%7D%5E%7B-1%7DV(t)-V(t_0)%7D%7Bt-t_0%7D.png)
%3DP_%7Bt_0t%7D(%5Cpartial_j(%5Cgamma(t_0)))%5Cin%20T_%7B%5Cgamma(t)%7DM.png)
%7DM%5Clongrightarrow%20T_%7B%5Cgamma(t)%7DM.png)
.png)
%3D%5Ctilde%7BV%7D%5Ej(t)%5Ctilde%7B%5Cpartial%7D_j(t).png)
%3D%5Ctilde%7BV%7D%5Ej(t_0)%5Ctilde%7B%5Cpartial%7D_j(t_0)%3DV%5Ej(t_0)%5Cpartial_j(%5Cgamma(t_0)).png)
-V(t_0)%7D%7Bt-t_0%7D%26%3D%26%5Cbigg(%5Clim_%7Bt%5Cto%20t_0%7D%5Cfrac%7B%5Ctilde%7BV%7D%5Ej(t)-%5Ctilde%7BV%7D%5Ej(t_0)%7D%7Bt-t_0%7D%5Cbigg)%5Cpartial_j(%5Cgamma(t_0))%5C%5C%0A%26%3D%26%5Cdot%7B%5Ctilde%7BV%7D%7D%5Ej(t_0)%5Cpartial_j(%5Cgamma(t_0)).png)
%3D%5Cdot%7B%5Ctilde%7BV%7D%7D(%5Cgamma(t_0))%5Cpartial_j(%5Cgamma(t_0))%5C%20(D_t%5Ctilde%7B%5Cpartial%7D_j%3D0).png)

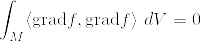
.png)
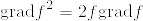
%3D2f%5CDelta%20f+2%7C%7C%7B%5Crm%20grad%7Df%7C%7C%5E2.png)


%5Ccong%20%5Cmathbf%7BR%7D.png)
%3D%5C%7B%5Comega%20%5Cin%5COmega%5Ep(S%5En):A%5E*%5Comega%3D%5Comega%5C%7D.png)
%3D%5C%7B%5Cpi%5E*%5Calpha:%5Calpha%5Cin%5COmega%5Ep(%5Cmathbf%7BR%7DP%5En)%5C%7D.png)
%3D%5COmega_%7Bsym%7D%5Ep(S%5En).png)
.png)
%5C%20s.t.%5C%20%5Cpi%5E*%5Comega%20%3D%5Ceta.png)
%5Ccong%200.png)
%5C%20s.t.%5C%20d%5Cgamma%20%3D%5Ceta.png)
%5C%20s.t.%5C%20%5Cpi%5E*%5Cbeta%3D%5Cgamma.png)
%3Dd%5Cgamma%3D%5Ceta%3D%5Cpi%5E*%5Comega.png)
%3D%5Cpi%5E*%5Comega.png)
%5Clongrightarrow%20%5COmega_%7Bsym%7D%5Ep(S%5En).png)
%5Ccong%200.png)
%5Ccong%20%5Cmathbf%7BR%7D%20%5CLongleftrightarrow%20M%20%7B%5Crm%5C%20is%5C%20orientable.%7D.png)
%5Ccong%20%5Cleft%0A%5C%7B%20%5Cbegin%7Barray%7D%7Bll%7D%0A%5Cmathbf%7BR%7D%20%26%20(n%5C%20%7B%5Crm%20:odd%7D)%5C%5C%20%0A0%20%26%20(n%5C%20%7B%5Crm%20:even%7D)%0A%5Cend%7Barray%7D%5Cright..png)



%5Ccirc%20(L_g%5Ccirc%20%5Cvarphi_%7Bs%7D%5Ccirc%20L_%7Bg%5E%7B-1%7D%7D).png)
)-f(g%5Ccdot%20g%5E%7B-1%7D%5Ccdot%20x)%7D%7Bt%7D.png)
(g%5E%7B-1%7D%5Ccdot%20x)%3D(L_g)_*X(f).png)

%5Ctimes%5C%7Bt%5C%7D%20:%20(a,b)%5Csubset%20%5Cmathbf%7BR%7D%5C%20%7B%5Crm%20open%5C%20interval%7D,%5C%20t%5Cin%20%5Cmathbf%7BR%7D.png)
%5Ctimes%20%5C%7Bt%5C%7D%5Cni%20(x,t)%5Cmapsto%20x%5Cin%20(a,b)%5Csubset%20%20%5Cmathbf%7BR%7D.png)
%5Cin%20%5Cmathbf%7BR%7D%5E3%5C%20%7C%5C%20a%3Cb,%5C%20t%5Cin%20%5Cmathbf%7BR%7D%5C%7D.png)
%3Dy.png)