a.s.収束と位相
Durrettの本に
Since there is a sequence of random variables that converges in probability but not a.s. , it follows that a.s. convergence does not come from a metric, or even from a topology.
とあった.
確率論の授業でも紹介されてた主張で,どう示すのかなと思っていたのだけれど,Durrettでは
Let 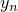 be a sequence of elements of a topological space. If every subsequence
be a sequence of elements of a topological space. If every subsequence %7D%0A.png) has a further subsequence
has a further subsequence %7D%0A.png) that converges to y then
that converges to y then  .
.
という主張から導けると書いてあった.
これからもしa.s.収束がある位相で定まると仮定して矛盾が導ける.確率収束する列から任意に部分列(確率収束する)をとって,Borel-Cantelliの補題からその確率収束先に概収束する部分列を取れる.概収束が位相から定まるという仮定と上の主張から,もとの確率収束する列は概収束する.これは矛盾.
という感じになる.
反例?
松島多様体で自明とあった補題.(前の記事参照→ Sardの定理 (続き) )
反例らしきものが出来たので.
まず多様体として  というものを考える.ただし
というものを考える.ただし 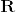 には通常の位相をいれ,
には通常の位相をいれ, 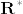 は
は 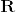 に離散位相を入れたものとし,多様体は直積位相をいれたものとする.
に離散位相を入れたものとし,多様体は直積位相をいれたものとする.
このとき  はHausdorff空間で(Hausdorff空間の直積はHausdorff空間になる),座標変換はRからRへの恒等写像のある開集合への制限であるから,これは1次元
はHausdorff空間で(Hausdorff空間の直積はHausdorff空間になる),座標変換はRからRへの恒等写像のある開集合への制限であるから,これは1次元 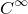 級多様体となる.
級多様体となる.
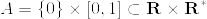 とすると,Aは
とすると,Aは  の測度0の集合であるが,
の測度0の集合であるが,%3D[0,1].png) でこれは測度0でない.よってこれが反例である.
でこれは測度0でない.よってこれが反例である.
なんか穴があるかもしれないけど,第二可算公理がないとやはりなんかダメな気がする.
臨界点
写像度の話を読んでいたら臨界点の集合が閉集合であることの証明を思いついたのでメモ.
M,Nを可微分多様体としそれぞれ次元をm,nとする.可微分写像f:M→Nとする.Mの正則点全体の集合が開集合であることを示せばよい.
m < nなら任意のMの点は臨界点であるから正則点全体は空集合であるから開である.
m >= nのとき.Mの任意の正則点xに対してxを含むあるMの座標近傍 ).png) とf(x)を含む
とf(x)を含む ).png) があって
があって
ただしDfは
.png)
を(i,j)成分にもつn×m行列である.rankがnなので _%7Bi,j%3D1,%5Ccdots,n%7D.png) が正則であるとしてよい.この行列式はR^mからRへの連続関数であるから
が正則であるとしてよい.この行列式はR^mからRへの連続関数であるから .png) の十分小さい近傍で0でない.つまりこの近傍上で
の十分小さい近傍で0でない.つまりこの近傍上で 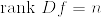 が成立している.これより正則点全体の集合をRとすれば,Rの任意の点は内点である.従ってRは開集合である.
が成立している.これより正則点全体の集合をRとすれば,Rの任意の点は内点である.従ってRは開集合である.
多様体の境界
今履修している幾何学の授業の演習問題で「境界付き多様体の境界の定義が局所座標によらないことを示せ」というのがあって,位相幾何の本見たら何やら難しいことが書いてあって萎えてたんだけどもっと簡単に示せることが調べたら分かった.
境界の定義は可微分多様体Mの座標近傍系を %5C%7D_%7B%5Calpha%5Cin%20A%7D.png) として Mの境界∂Mは
として Mの境界∂Mは
ただし %5Cin%5Cmathbf%7BR%7D%5En%5C%20%7C%5C%20x_n%5Cgeq%200%5C%7D.png) ,
,%5Cin%5Cmathbf%7BR%7D%5En%5C%20%7C%5C%20x_n%3D%200%5C%7D.png) とする.これが局所座標によらない,つまりxの座標近傍
とする.これが局所座標によらない,つまりxの座標近傍 ,%20%5C%20(U_%7B%5Cbeta%7D,%5Cvarphi_%7B%5Cbeta%7D).png) に対して
に対して
これを待遇を用いて
を示せばよい.座標変換は全単射なので座標変換のヤコビ行列は正則.よって逆関数定理から座標変換は局所同型..png) の開近傍を十分小さくとれば,その座標変換による像は
の開近傍を十分小さくとれば,その座標変換による像は 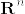 の開集合にうつる.よって
の開集合にうつる.よって%5Cnot%5Cin%20%5Cpartial%20%5Cmathbf%7BH%7D%5En.png) .
.
そういえばMilnorの本が届いた.
%3D%5Csup%5C%7By%5Cin%5Cmathbf%7BR%7D:F(y)%5Cleq%5Comega%5C%7D.png)
%5Cleq%20a%5CLongleftrightarrow%20x%5Cleq%20Y(a).png)
%3E%20a%5CLongleftrightarrow%20x%3E%20Y(a).png)
.png)
%3CY(%5Comega).png)
)%5Cgeq%20F(Y(%5Comega_n))%5Cgeq%20%5Comega_n%20.png)
)%3C%20%5Comega.png)
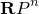
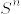

%5Ccong%20%5Cmathbf%7BR%7D.png)
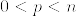
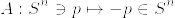
%3D%5C%7B%5Comega%20%5Cin%5COmega%5Ep(S%5En):A%5E*%5Comega%3D%5Comega%5C%7D.png)
%3D%5C%7B%5Cpi%5E*%5Calpha:%5Calpha%5Cin%5COmega%5Ep(%5Cmathbf%7BR%7DP%5En)%5C%7D.png)
%3D%5COmega_%7Bsym%7D%5Ep(S%5En).png)
.png)
%5C%20s.t.%5C%20%5Cpi%5E*%5Comega%20%3D%5Ceta.png)
%5Ccong%200.png)
%5C%20s.t.%5C%20d%5Cgamma%20%3D%5Ceta.png)
%5C%20s.t.%5C%20%5Cpi%5E*%5Cbeta%3D%5Cgamma.png)
%3Dd%5Cgamma%3D%5Ceta%3D%5Cpi%5E*%5Comega.png)
%3D%5Cpi%5E*%5Comega.png)
%5Clongrightarrow%20%5COmega_%7Bsym%7D%5Ep(S%5En).png)
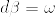
%5Ccong%200.png)
%5Ccong%20%5Cmathbf%7BR%7D%20%5CLongleftrightarrow%20M%20%7B%5Crm%5C%20is%5C%20orientable.%7D.png)
%5Ccong%20%5Cleft%0A%5C%7B%20%5Cbegin%7Barray%7D%7Bll%7D%0A%5Cmathbf%7BR%7D%20%26%20(n%5C%20%7B%5Crm%20:odd%7D)%5C%5C%20%0A0%20%26%20(n%5C%20%7B%5Crm%20:even%7D)%0A%5Cend%7Barray%7D%5Cright..png)
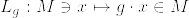
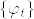
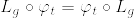
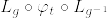
%5Ccirc%20(L_g%5Ccirc%20%5Cvarphi_%7Bs%7D%5Ccirc%20L_%7Bg%5E%7B-1%7D%7D).png)
)-f(g%5Ccdot%20g%5E%7B-1%7D%5Ccdot%20x)%7D%7Bt%7D.png)
(g%5E%7B-1%7D%5Ccdot%20x)%3D(L_g)_*X(f).png)
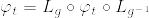
%5Ctimes%5C%7Bt%5C%7D%20:%20(a,b)%5Csubset%20%5Cmathbf%7BR%7D%5C%20%7B%5Crm%20open%5C%20interval%7D,%5C%20t%5Cin%20%5Cmathbf%7BR%7D.png)
%5Ctimes%20%5C%7Bt%5C%7D%5Cni%20(x,t)%5Cmapsto%20x%5Cin%20(a,b)%5Csubset%20%20%5Cmathbf%7BR%7D.png)
%5Cin%20%5Cmathbf%7BR%7D%5E3%5C%20%7C%5C%20a%3Cb,%5C%20t%5Cin%20%5Cmathbf%7BR%7D%5C%7D.png)
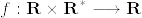
%3Dy.png)
%5Cin%20%5Cpartial%20%5Cmathbf%7BH%7D%5En%5C%7D.png)
%5Cin%20%5Cpartial%20%5Cmathbf%7BH%7D%5CLongrightarrow%20%5Cvarphi_%7B%5Cbeta%7D(x)%5Cin%20%5Cpartial%20%5Cmathbf%7BH%7D.png)
%5Cnot%5Cin%20%5Cpartial%20%5Cmathbf%7BH%7D%5En%20%5CLongrightarrow%20%5Cvarphi_%7B%5Calpha%7D(x)%5Cnot%5Cin%20%5Cpartial%20%5Cmathbf%7BH%7D%5En.png)