多様体上の調和関数
Mをコンパクト,連結,向きづけられた境界付き可微分多様体とする.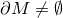 であるとする.M上の調和関数u,vが境界上で一致するときuとvはM上で一致する.
であるとする.M上の調和関数u,vが境界上で一致するときuとvはM上で一致する.
という主張の証明のメモ.
u-vを考えれば良いから,調和関数fで境界上で0となるものが,M上で恒等的に0になることを示せばよい. をMの体積要素とする.Stokesの定理から
をMの体積要素とする.Stokesの定理から
ただし境界にはMから定まる向きを入れ,Nは外向きの単位ベクトルとし,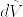 は境界の体積要素とする.fは調和で境界上で0となるから
は境界の体積要素とする.fは調和で境界上で0となるから
よって 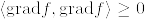 より
より 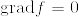 .ゆえにfは定数関数(任意のベクトル場Xに対してXf=0より).仮定より境界上で0で,Mは連結であったからf=0となる.
.ゆえにfは定数関数(任意のベクトル場Xに対してXf=0より).仮定より境界上で0で,Mは連結であったからf=0となる.
似たような主張で「Mの境界が空であったら調和関数は定数に限る(Mは向き付可能でなくても良い)」というのが松島多様体にあった.そちらもgrad fが0となることを示すために 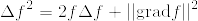 という式をつかい,ストークスの定理から導いていた.細かいけど
という式をつかい,ストークスの定理から導いていた.細かいけど  ではないだろうか.計算すると
ではないだろうか.計算すると
よって
となるから
となる気がするのだけど・・・
X,Yは実確率変数とし,任意の実数aに対しP(X=a)=0,またXとYは独立で同分布に従うとする.このときP(X=Y)=0となる.
タイトルの主張は確率論のテストで必要だった主張です.テストの時は分かりませんでした.
ですが,零集合の非可算和は零集合とは限らないのでこれではうまくいかないです.
そこでFubiniの定理を使います.P^Xを像測度とするとき,XとYは独立であるから, %7D%3DP%5EX%5Cotimes%20P%5EY.png) であり,非負値可測関数に対してFubiniの定理がなりたつから
であり,非負値可測関数に対してFubiniの定理がなりたつから
となる.
であるから
となる.
Sardの定理の証明を読んでいて,R^nの部分集合Aが,任意の超平面{p}×R^{n-1}と共通部分をとったとき,そのn-1次元ルベーグ測度が0ならば,Aのn次元ルベーグ測度が0 というのをFubiniの定理から示していて,それのおかげでやっと解決しました.
どうでもいいのですがミルナーの本は添字が見づらいです.
fully T_4 ⇒ T_4
fully T_4 ⇒ T_4 の証明を思いついたのでメモ. (fully T_4 の定義は任意の開被覆に対して open star refinementが存在する.)
対遇をとって T_4 でない ⇒ fully T_4 でない ことを示す.
T_4でないとするとある互いに素な閉集合F_1,F_2があって,F_1,F_2を含む任意の開集合O_1⊃F_1, O_2⊃F_2に対して となる.開被覆
となる.開被覆 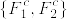 を考える.fully T_4であるとする.点xのopen star refinement を
を考える.fully T_4であるとする.点xのopen star refinement を 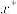 とする.このとき
とする.このとき
であるから仮定よりあるF_1の点a_1とF_2の点a_2があって
 の点aをとる.open star refinement の定義から
の点aをとる.open star refinement の定義から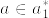 より
より 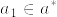 ,また
,また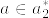 より
より 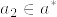 となるから
となるから 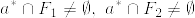 となる.ところが
となる.ところが  は
は 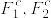 のいずれにも含まれないから矛盾.よってfully T_4ではない.
のいずれにも含まれないから矛盾.よってfully T_4ではない.
Scheffe's Lemma
David Williamsの『Probability with martingales』という本(下のやつ)のChapter5にあるScheffeの補題(5.10)のところにあるExerciseの証明のメモです.
 | Probability with Martingales (Cambridge Mathematical Textbooks) (1991/02/14) David Williams 商品詳細を見る |
まずFatouの補題より
また
より

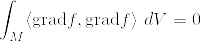
.png)
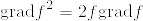
%3D2f%5CDelta%20f+2%7C%7C%7B%5Crm%20grad%7Df%7C%7C%5E2.png)
%3DP(%5Cbigcup_%7Ba%5Cin%20%5Cmathbf%7BR%7D%7D%20%5C%7B%20X%3DY%3Da%20%5C%7D%20).png)
%26%3D%26%5Cint_%7B%5COmega%7D1_%7B%5C%7BX%3DY%5C%7D%7D(%5Comega)dP(%5Comega)%5C%5C%0A%26%3D%26%5Cint_%7B%5Cmathbf%7BR%7D%7D%5Cbigg(%5Cint_%7B%5Cmathbf%7BR%7D%7D1_%7B%5C%7Bx%3Dy%5C%7D%7D(x,y)dP%5EX(x)%5Cbigg)dP%5EY(y).png)
dP%5EX(x)%3DP(X%3Dy)%3D0.png)
%3D%5Cint_%7B%5Cmathbf%7BR%7D%7D%5C%200%5C%20dP%5EY(y)%3D0.png)
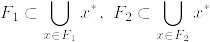
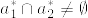
%3D%5Cbigg%5C%7B%20%5Comega:%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7B2%5En%7D%5Csup_%7B0%5Cleq%20t%5Cleq%20n%20,%20t%5Cin%20%5Cmathbf%7BQ%7D%7D(%7C%5Comega(t)-%5Comega_0(t)%7C%5Cwedge%201)%3C%5Cvarepsilon%5Cbigg%5C%7D.png)

%5Cni%20%5Comega%20%5Cmapsto%20%5Comega(t)%5Cin%20%5Cmathbf%7BR%7D%20.png)
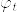
%5Cni%20%5Comega%20%5Cmapsto%20%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7B2%5En%7D%5Csup_%7B0%5Cleq%20t%5Cleq%20n,%20t%5Cin%5Cmathbf%7BQ%7D%7D(%7C%5Comega(t)-%5Comega_0(t)%7C%5Cwedge%201)%5Cin%20%5Cmathbf%7BR%7D.png)
%3D%5C%7B%5Cvarphi(%5Comega)%3C%5Cvarepsilon%5C%7D.png)
.png)
%5Cto%20%5Cmu(f%5E%7B%5Cpm%7D).png)
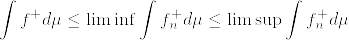
.png)
d%5Cmu%5C%5C%0A%26%5Cleq%20%26%20%5Climsup_n%20%5Cint%20(f_n%5E+-f%5E+)d%5Cmu+%5Climinf%5Cint%20(f_n%5E-%20-f%5E-)d%5Cmu%5C%5C%0A%26%5Cleq%20%26%20%5Climsup%5Cint%20%5C%7B(f_n%5E+-f%5E+)+(f_n%5E--f%5E-)%5C%7Dd%5Cmu%5C%5C%0A%26%5Cleq%20%26%20%5Climsup%5Cint%20%7Cf_n%7Cd%5Cmu%20-%5Cint%20%7Cf%7Cd%5Cmu%3D0.png)
%5Cto%20%5Cmu(f%5E%7B+%7D).png)
%5Cto%20%5Cmu(f%5E%7B-%7D).png)
%3D%5Csup%5C%7By%5Cin%5Cmathbf%7BR%7D:F(y)%5Cleq%5Comega%5C%7D.png)
%5Cleq%20a%5CLongleftrightarrow%20x%5Cleq%20Y(a).png)
%3E%20a%5CLongleftrightarrow%20x%3E%20Y(a).png)
.png)
%3CY(%5Comega).png)
)%5Cgeq%20F(Y(%5Comega_n))%5Cgeq%20%5Comega_n%20.png)
)%3C%20%5Comega.png)
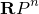


%5Ccong%20%5Cmathbf%7BR%7D.png)
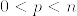
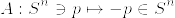
%3D%5C%7B%5Comega%20%5Cin%5COmega%5Ep(S%5En):A%5E*%5Comega%3D%5Comega%5C%7D.png)
%3D%5C%7B%5Cpi%5E*%5Calpha:%5Calpha%5Cin%5COmega%5Ep(%5Cmathbf%7BR%7DP%5En)%5C%7D.png)
%3D%5COmega_%7Bsym%7D%5Ep(S%5En).png)
.png)
%5C%20s.t.%5C%20%5Cpi%5E*%5Comega%20%3D%5Ceta.png)
%5Ccong%200.png)
%5C%20s.t.%5C%20d%5Cgamma%20%3D%5Ceta.png)
%5C%20s.t.%5C%20%5Cpi%5E*%5Cbeta%3D%5Cgamma.png)
%3Dd%5Cgamma%3D%5Ceta%3D%5Cpi%5E*%5Comega.png)
%3D%5Cpi%5E*%5Comega.png)
%5Clongrightarrow%20%5COmega_%7Bsym%7D%5Ep(S%5En).png)
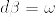
%5Ccong%200.png)
%5Ccong%20%5Cmathbf%7BR%7D%20%5CLongleftrightarrow%20M%20%7B%5Crm%5C%20is%5C%20orientable.%7D.png)
%5Ccong%20%5Cleft%0A%5C%7B%20%5Cbegin%7Barray%7D%7Bll%7D%0A%5Cmathbf%7BR%7D%20%26%20(n%5C%20%7B%5Crm%20:odd%7D)%5C%5C%20%0A0%20%26%20(n%5C%20%7B%5Crm%20:even%7D)%0A%5Cend%7Barray%7D%5Cright..png)