Problem3.5.7
Problem3.5.7
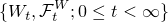 を一次元のブラウン運動とする.ただしフィルとレーションはWを可測にする最小のσ加法族とする.Tを
を一次元のブラウン運動とする.ただしフィルとレーションはWを可測にする最小のσ加法族とする.Tを.png) -stopping time でかつ,
-stopping time でかつ,%3D1.png) を満たすものとする.このときWaldの恒等式
を満たすものとする.このときWaldの恒等式
が成立することと,
として定義したものを 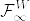 に一意的に拡張した測度である(Karatzas and Shreve, Corollary 3.5.2参照).
に一意的に拡張した測度である(Karatzas and Shreve, Corollary 3.5.2参照).
は上の条件を満たす.(Novikov conditionの証明に用いられる(Proposition 3.5.12))
[証明]
Optional Sampling Theoremから
よって単調収束定理から
特に, なら
なら  なので
なので %5Cleq%20P(S_b%3C%5Cinfty)%3D1.png) で
で %7D.png) のもとで,
のもとで,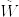 はブラウン運動になる(Girsanovの定理)ので
はブラウン運動になる(Girsanovの定理)ので
[証明終]
Xを時間に関して一様でないマルコフ過程とするとき,(t,X_t)は時間に関して一様なマルコフ過程となる.
ChapterIII Exercise(1.11) (Revuz-Yor)
Xが時間に関して一様でないE値マルコフ過程とするとき,(t,X_t)は時間に関して一様なR_+×E値マルコフ過程となる(これを"time-space" processと呼ぶ)ことを示せ. またこのとき,推移関数(transition function)を書き下せ.
[証明]
Xは時間に関して一様でないマルコフ過程なので,あるフィルター付き確率空間 ,Q).png) で Xは
で Xは .png) に適合し,任意の有界な非負値可測関数 f,
に適合し,任意の有界な非負値可測関数 f,  , 推移関数
, 推移関数 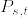 で
で
が成立している.初期測度を 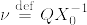 とする.Thorem(1,4)[Revuz-Yor, p81]より,任意の
とする.Thorem(1,4)[Revuz-Yor, p81]より,任意の 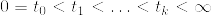 と非負値有界可測関数 f_i に対して
と非負値有界可測関数 f_i に対して
が成立している.ここで %5Cotimes%20%5Cmathcal%7BE%7D).png) 上の確率測度を次のように定義する.
上の確率測度を次のように定義する.%5Cin%20%5Cmathbf%7BR%7D_+%5Ctimes%20E,%5Cquad%20A%5Ctimes%20B%5Cin%20%5Cmathcal%7BB%7D(%5Cmathbf%7BR%7D_+)%5Ctimes%20%5Cmathcal%7BE%7D.png) に対して
に対して
つまり, ,%5Ccdot)%3D%5Cdelta_%7Bu+t-s%7D%5Cotimes%20P_%7Bu,u+t-s%7D(x,%5Ccdot).png) とする.このとき,R_{t,s} は時間に関して一様である.つまり,
とする.このとき,R_{t,s} は時間に関して一様である.つまり,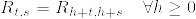 が成立する.
が成立する. 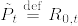 とすると,Fubiniの定理より
とすると,Fubiniの定理より 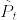 は推移関数となる.また 任意の
は推移関数となる.また 任意の 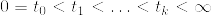 と非負値有界可測関数 f_i, g_i に対して
と非負値有界可測関数 f_i, g_i に対して
となることもFubiniの定理から分かる.%5Cotimes%20%5Cmathcal%7BE%7D.png) 可測関数を単関数近似して,一般の有界非負値可測関数について上と同じ等式を得るので,再びThorem(1,4)[Revuz-Yor, p81]より(t,X_t)は時間に関して一様なマルコフ過程となる.[証明終]
可測関数を単関数近似して,一般の有界非負値可測関数について上と同じ等式を得るので,再びThorem(1,4)[Revuz-Yor, p81]より(t,X_t)は時間に関して一様なマルコフ過程となる.[証明終]
少し混乱してR_{s,t}を定義するのに苦労しました.
LCH,second countableな空間の点を分離する非負値C_0関数列
主張
Eを局所コンパクトハウスドルフ(以下LCHと略す)かつ第2可算公理を満たす空間とし,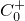 をE上の非負値連続関数で無限遠点で消える関数全体とする.このとき関数列
をE上の非負値連続関数で無限遠点で消える関数全体とする.このとき関数列 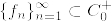 で任意の相異なるEの2点x,yに対してあるf_nがあってf_n(x)≠f_n(y)となるものが存在する.
で任意の相異なるEの2点x,yに対してあるf_nがあってf_n(x)≠f_n(y)となるものが存在する.
補題
Eが主張の条件を満たすとき,Eの任意の開集合Oはσコンパクトである.
[補題の証明]
次の事実を用いる.
事実
XがLCHであり,K⊂U⊂XでKはコンパクト,Uは開集合であるとき,相対コンパクトな開集合Vが存在して 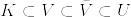 となる.(Folland, 猪狩参照)
となる.(Folland, 猪狩参照)
これから任意のx∈Oに対してある開近傍V_xが存在して 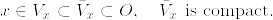 となる.
となる. をEの可算開基とすると,
をEの可算開基とすると,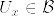 で
で  となるものが存在する.従って
となるものが存在する.従って  となる.以上より
となる.以上より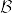 は可算であるから,Oはσコンパクトである.[補題証明終]
は可算であるから,Oはσコンパクトである.[補題証明終]
[主張の証明]
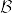 をEの可算開基とし,
をEの可算開基とし,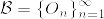 とする.各O_nは上の補題からσコンパクトであるから
とする.各O_nは上の補題からσコンパクトであるから
となるものが存在する.%7D%5C%7D_%7Bj,n%5Cin%20%5Cmathbf%7BN%7D%7D.png) が主張にある関数列の条件を満たすことはEがハウスドルフで,開基の元で2点を分離できることから明らか.[証明終]
が主張にある関数列の条件を満たすことはEがハウスドルフで,開基の元で2点を分離できることから明らか.[証明終]
Yorの本だと証明のなかでこれを使うのですが,主張だけ書いてあって証明はなかったので自分で付けてみました.少し回りくどい気もします.
正則+第2可算公理⇒正規
主張
正則(ハウスドルフ性を入れなくても良い)でかつ第2可算公理を満たす空間は,正規である.
[証明]
内田先生の集合と位相の本の演習問題(p107)になっていて,そこにある方針で示します.以下A,Bを互いに交わらない閉集合とする.
(1)開集合系{U_n}, {V_n}で
となり,さらに,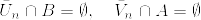 となるものが存在する.実際第2可算公理を満たすから可算開基を
となるものが存在する.実際第2可算公理を満たすから可算開基を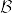 とすると,正則であることからAの任意の点xに対して,
とすると,正則であることからAの任意の点xに対して,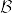 の元 U_x と 開集合 O_x で
の元 U_x と 開集合 O_x で
となる.同様にすればV_nも取れる.
(2) (1)の{U_n}, {V_n}に対して
とする.明らかにU,Vは開集合である.また .png) より
より 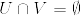 である.そして
である.そして
である.実際(1)より任意のx∈Aに対してあるNがあってx∈U_N.  より,
より,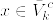 . よって x∈U'_n⊂U となる.B,Vの方も同様.[証明終]
. よって x∈U'_n⊂U となる.B,Vの方も同様.[証明終]
この主張から正則,第2可算公理,ハウスドルフを満たす空間は距離付け可能であることがわかります.
Exercise5.2.27
Exercise5.2.27
次の1次元確率微分方程式の解を陽に求めよ.
ただし,Wは1次元ブラウン運動とする.
[解]
%3D%5Csigma(x)%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Csqrt%7B1+x%5E2%7D.png) とすると,この確率微分方程式は
とすると,この確率微分方程式は
の解となる.σ(x)は2階連続微分可能で1階微分,2階微分ともにR上で有界である.b(x)も同様であるから,特にLipschitz連続である.従ってKaratzasShreve Proposition5.2.21より,次の常微分方程式を解くことで上の確率微分方程式の解を得ることができる.
ただし,
これを解いて
以上より解は
となる.[終]
ある種の確率微分方程式が常微分方程式を解くことで解を得ることができるという話題でした.上の場合f(x,y)がxによらないので楽でした.これがxによると常微分方程式を陽に解くことができないので,解析解は出ないように思います.
局所コンパクトハウスドルフ空間上では,ある連続関数の列でG-δコンパクト集合の定義関数に各点収束するものが存在する.
主張
局所コンパクトハウスドルフ(以下LCHとする)X上では,ある連続関数の列でG-δコンパクト集合Kの定義関数に各点収束するものが存在する.
[証明]
次の事実を用いる.
事実
LCHのコンパクト集合Kと開集合OでK⊂Oならば,コンパクト台をもつ実数値連続関数で 0≦u(x)≦1,u(x)=1 (x∈K),supp(u)⊂O となるものが存在する. (猪狩「実解析入門」6章などを参照)
.png) とする.上の事実から各nに対してコンパクト台をもつ連続関数の列
とする.上の事実から各nに対してコンパクト台をもつ連続関数の列 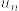 で
で
となるものが存在する.このとき
となる.実際任意のnで  とすると,
とすると, 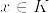 となり矛盾.このnにたいして,
となり矛盾.このnにたいして,%3D0.png)
さらにXが第二可算公理を満たすとコンパクトG_δ集合を含む最小のσ加法族はボレル集合族に一致します.
]%3D1.png)
%7D(T%3C%5Cinfty)%3D1.png)
%5Cquad%20(%5Cmu%5Cneq%200).png)
%7D(A)%3DE[1_AZ_t];%5Cquad%20A%5Cin%20%5Cmathcal%7BF%7D_t%5EW.png)
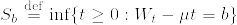
%7D[T%5Cleq%20t]%5Cquad%20(0%5Cleq%20t%3C%5Cinfty)%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DZ_t]%20%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DE[Z_t%7C%5Cmathcal%7BF%7D_%7Bt%5Cwedge%20T%7D]]%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DZ_%7Bt%5Cwedge%20T%7D]%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DZ_T].png)
%7D(T%3C%5Cinfty)%3DE[Z_T]%3DE[%5Cexp%20(%5Cmu%20W_T-%5Cfrac%7B1%7D%7B2%7D%5Cmu%20%5E2%20T)].png)
%7D(S_b%3C%5Cinfty)%3DP%5E%7B(%5Cmu)%7D(%5Cinf%5C%7Bt%5Cgeq%200:%5Ctilde%7BW%7D_t%3Db%5C%7D)%3D1.png)
.png)
%3De%5E%7B-b%5Csqrt%7B2%5Calpha%7D%7D;%5Cquad%20b%3E0,%5Calpha%3E0.png)
.png)
)%3D0%5Cquad%20%7B%5Crm%20a.s.%7D.png)
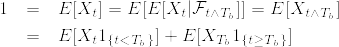
%3D1,%5Cquad%20%5Clim_%7Bt%5Cto%5Cinfty%7DX_t%3D0%5Cquad%20%7B%5Crm%20a.s.%7D,%5Cquad%20%20%7C1_%7B%5C%7Bt%3CT_b%5C%7D%7DX_t%7C%5Cleq%20e%5E%7B%5Clambda%20b%7D.png)
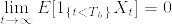
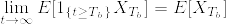
]%3D1.png)
%7C%5Cmathcal%7BG%7D_s]%3DP_%7Bs,t%7Df(X_s)%5Cquad%20%20Q%7B%5Crm%20-%5C%20a.s.%7D.png)
%5Cbigg]%5C%5C%0A%26%26%3D%5Cint_E%5Cnu(dx_0)f_0(x_0)%5Cint_EP_%7B0,t_1%7D(x_0,dx_1)f_1(x_1)%5Cldots%20%5Cint_EP_%7Bt_%7Bk-1%7D,t_k%7D(x_%7Bk-1%7D,dx_k)f_k(x_k).png)
,A%5Ctimes%20B)%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Cdelta_%7Bu+t-s%7D(A)P_%7Bu,u+t-s%7D(x,B)%5Cquad%20(%5Cdelta:%7B%5Crm%20Dirac%5C%20measure%7D).png)
g_i(X_%7Bt_i%7D)%5Cbigg]%3D%5C%5C%0A%26%26%5Cint_%7B%5Cmathbf%7BR%7D_+%5Ctimes%20E%7D%5Cdelta_0%5Cotimes%5Cnu%20(ds_0%5Cotimes%20dx_0)f_0(s_0)g_0(X_0)%5Cint_%7B%5Cmathbf%7BR%7D_+%5Ctimes%20E%7D%5Ctilde%7BP%7D_%7Bt_1%7D((s_0,x_0),dt_1%5Cotimes%20dx_1)f_1(s_1)g_1(X_%7Bt_1%7D)%5Cldots%20%5C%5C%0A%26%26%5Cint_E%5Ctilde%7BP%7D_%7Bt_k-t_%7Bk-1%7D%7D((s_%7Bk-1%7D,%20x_k),ds_k%5Cotimes%20dx_k)f_k(s_k)g_k(x_k).png)
%7D%5Cquad%20(K_j%5E%7B(n)%7D%20%7B%5Crm%5C%20is%5C%20compact%7D.).png)
%7D%5Cin%20C_0%5E+.png)
%7D(x)%3D1(%20x%5Cin%20K_j%5E%7B(n)%7D),%5Cquad%20%7B%5Crm%20supp%7Df_j%5E%7B(n)%7D%5Csubset%20O_n,%5Cquad%200%5Cleq%20f_j%5E%7B(n)%7D(x)%5Cleq%201%20(%5Cforall%7Bx%7D%5Cin%20E).png)
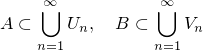

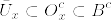
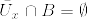
.png)


dt%20+%20%5Csqrt%7B1+X_t%5E2%7D%5C%20dW_t,%5Cquad%20P(X_0%3D%5Cxi)%3D1.png)
+%5Cfrac%7B1%7D%7B2%7D%5Csigma(X_s)%5Csigma'(X_s)%5Cbigg%5C%7Dds+%5Cint_0%5Et%5Csigma(X_s)dW_s.png)
,%5Cquad%20u(0,y)%3Dy..png)
%3Df(W_t(%5Comega),Y_t(%5Comega))%5Cquad%20%7B%5Crm%20with%7D%5Cquad%20Y_0(%5Comega)%3D%5Cxi(%5Comega).png)
%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Cfrac%7B1%7D%7B%5Crho%20(x,y)%7D,%5Cquad%20f(x,y)%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Crho(x,y)b(u(x,y))..png)
%3D%5Cfrac%7B1%7D%7B2%7D%5Cbigg%5C%7B(%5Csqrt%7B1+y%5E2%7D+y)e%5Ex-(%5Csqrt%7B1+y%5E2%7D-y)e%5E%7B-x%7D%5Cbigg%5C%7D.png)
%3D%5Csqrt%7B1+y%5E2%7D.png)
%3D%5Cfrac%7B1%7D%7B2%7D%5Cbigg%5C%7B(%5Csqrt%7B1+%5Cxi%5E2(%5Comega)%7D+%5Cxi(%5Comega))e%5Et-(%5Csqrt%7B1+%5Cxi%5E2(%5Comega)%7D-%5Cxi(%5Comega))e%5E%7B-t%7D%20%5Cbigg%5C%7D.png)
%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B2%7D%5Cbigg%5C%7B(%5Csqrt%7B1+Y_t%5E2%7D+Y_t)e%5E%7BW_t%7D-(%5Csqrt%7B1+Y_t%5E2%7D-Y_t)e%5E%7B-W_t%7D%20%5Cbigg%5C%7D%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B2%7D%5Cbigg%5C%7B(%5Csqrt%7B1+%5Cxi%5E2%7D+%5Cxi)e%5E%7Bt+W_t%7D%20-(%5Csqrt%7B1+%5Cxi%5E2%7D-%5Cxi)e%5E%7B-t-W_t%7D%5Cbigg%5C%7D.png)
%5Csubset%20%5Cbigcap_%7Bi%3D1%7D%5EnO_i,%5Cquad%20u_n(x)%3D1%5Cquad%20(x%5Cin%20K).png)
%3D%5Cleft%5C%7B%0A%5Cbegin%7Barray%7D%7Bll%7D%0A1%5Cquad%20(x%5Cin%20K)%5C%5C%0A0%5Cquad%20(x%5Cnot%5Cin%20K)%0A%5Cend%7Barray%7D%0A%5Cright..png)
%3D1%5Cquad%20(x%5Cin%20K).png)
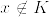
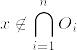
%3D0%5Cquad(x%5Cnot%20%5Cin%20K).png)