Exercise5.2.17(Ito-Watanabe(1978))
Problem3.3.23
Problem3.3.23
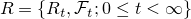 をd(≧3)次元のr(>0)を出発するベッセル過程とする.
をd(≧3)次元のr(>0)を出発するベッセル過程とする. 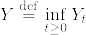 とするとき,
とするとき,
となることを示せ.つまりYはベータ分布に従う.
[証明]
伊藤の公式より,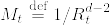 は局所連続マルチンゲールである.従ってあるstopping timeの列
は局所連続マルチンゲールである.従ってあるstopping timeの列  で
で %7D%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7DM_%7BT_n%5Cwedge%20t%7D.png) がマルチンゲールとなり,
がマルチンゲールとなり, となるものが存在する.
となるものが存在する. %7D%5Cgeq%201/x%5E%7Bd-2%7D%5C%7D.png) ,
, 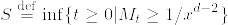 とすると,これらはstopping timeで,
とすると,これらはstopping timeで,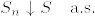 となる.
となる.
で, %7D1_%7B%5C%7BS_n%3D%5Cinfty%5C%7D%7D%7C%5Cleq%201/x%5E%7Bd-2%7D.png) ,
, %7D1_%7B%5C%7B0%3CS_n%3C%5Cinfty%5C%7D%7D%7C%3C1/x%5E%7Bd-2%7D.png) より条件付き期待値のルベーグの収束定理より,
より条件付き期待値のルベーグの収束定理より,
整理して
を得る.[証明終]
Exercise(3.12),Chapter2(Revuz, Yor)続き
つまり
つまり
となる.
(4) )%5Cquad%20(%5Cmu%20%3E0).png) がマルチンゲールであることはすぐにわかる.
がマルチンゲールであることはすぐにわかる. 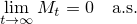 であることを示す.非負のマルチンゲールであるから,
であることを示す.非負のマルチンゲールであるから, 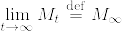 が存在する.Fatouの補題から
が存在する.Fatouの補題から
となり 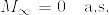 である.よって(1)より
である.よって(1)より %5Cgeq%20x)%3DP(M%5E*%5Cgeq%20%5Cexp(2%5Cmu%20x))%3D%5Cexp(-2%5Cmu%20x).png) となり,結論を得る.[証明終]
となり,結論を得る.[証明終]
Revuz and YorのContinuous Martingales and Brownian Motionという本の問題でした.この問題を使って3次元以上のベッセル過程で0が非再帰的であることが示せるそうなので考えています.今後もこの本の問題を解くかわかりませんが,この本の問題のカテゴリはRevuzAndYorにしておきます.
Exercise(3.12),Chapter2(Revuz, Yor)
Exercise(3.12),Chapter2(Revuz, Yor)
Mを正の値を取る連続マルチンゲールとし,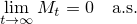 とする.また
とする.また 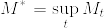 とおく.
とおく.
(1) 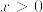 に対して
に対して .png) となることを示せ.
となることを示せ.
(2) より一般に 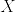 が 正の値を取る
が 正の値を取る 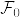 可測な確率変数であるとき
可測な確率変数であるとき .png) であることを示せ.
であることを示せ.
(3) B を .png) を出発する1次元のブラウン運動であるとする.
を出発する1次元のブラウン運動であるとする.  とするとき,
とするとき,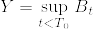 の分布を求めよ.
の分布を求めよ.
(4) B を標準ブラウン運動であるとする. )%5Cquad%20(%5Cmu%20%3E0).png) を用いて
を用いて .png) がパラメータ
がパラメータ 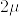 の指数分布に従うことを示せ.
の指数分布に従うことを示せ.
[証明]
(1)  とすると,これはstopping timeでありMはマルチンゲールであるから,
とすると,これはstopping timeでありMはマルチンゲールであるから, もマルチンゲールである.よって
もマルチンゲールである.よって 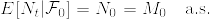 となる.ここで
となる.ここで
%7C%3C%20x%20%5Cquad%20%5Cforall%7Bt%7D.png) ,
,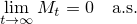 であるから条件付き期待値のルベーグの収束定理より
であるから条件付き期待値のルベーグの収束定理より
となる.一方
となり,
となる.2つ目の等式は  であることと条件付き期待値のルベーグの収束定理から従う.以上より
であることと条件付き期待値のルベーグの収束定理から従う.以上より
よって
[(1)の証明終][次の記事に続きます]
一様可積分かつ局所連続マルチンゲールであるがマルチンゲールでない例2(M.Yor)
一様可積分かつ局所連続マルチンゲールであるがマルチンゲールでない例(M.Yor)
上の記事で一様可積分かつ局所連続マルチンゲールであるがマルチンゲールでない例を調べたのですが,からしゅれでは次のExerciseでまたこれと同じ種類の例を挙げているので,証明します.
Exercise3.3.37
Rを0を出発する2次元のベッセル過程とする.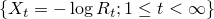 が局所連続マルチンゲールで
が局所連続マルチンゲールで
が成立することを示せ.また 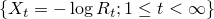 はマルチンゲールでないことも示せ.(一様可積分であることもわかる.)
はマルチンゲールでないことも示せ.(一様可積分であることもわかる.)
[証明]
まず局所連続マルチンゲールであることを示す.伊藤の公式から
これより 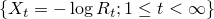 は局所連続マルチンゲールである.ただしBは1次元の標準ブラウン運動である.
は局所連続マルチンゲールである.ただしBは1次元の標準ブラウン運動である.
ただしn次元球の体積を用いて積分を評価した(一様可積分かつ局所連続マルチンゲールであるがマルチンゲールでない例(M.Yor)参照).α<0のときは, .png) として
として
これより
となる.次に一様可積分であることを示す.そのために任意の 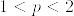 に対してL^p有界であることを示す.つまり
に対してL^p有界であることを示す.つまり
を示す.
よって
となる.これより一様可積分である.最後にマルチンゲールでないことを背理法を用いて示す.マルチンゲールであれば期待値が一定であるから
exponential supermartingale
Problem3.2.28
 をstandard Brownian motion とし
をstandard Brownian motion とし 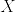 をmeasurable,adaptedで
をmeasurable,adaptedで
を満たす確率過程とする.つまり確率積分
は定義できるものとする.このとき
と定義する. ),%5Cmathcal%7BF%7D_t;0%5Cleq%20t%3C%5Cinfty%5C%7D.png) は優マルチンゲールであることを示せ.また
は優マルチンゲールであることを示せ.また 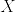 が単過程のときマルチンゲールであることを示せ.
が単過程のときマルチンゲールであることを示せ.
[証明]
まず 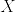 が単過程のときマルチンゲールであることを示す.
が単過程のときマルチンゲールであることを示す. 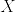 が単過程のとき
が単過程のとき  に対して
に対して
と表せる.ただし 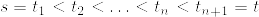 とした.また単過程の定義よりある定数Mが存在して
とした.また単過程の定義よりある定数Mが存在して
であり, 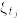 は
は  可測である.前の記事の補題より
可測である.前の記事の補題より
これと条件付き期待値のtower propertyから
が成立する.よって
これより 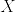 が単過程のときマルチンゲールである.
が単過程のときマルチンゲールである.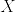 が単過程でないときは伊藤の公式より
が単過程でないときは伊藤の公式より
よって ),%5Cmathcal%7BF%7D_t;0%5Cleq%20t%3C%5Cinfty%5C%7D.png) は非負値局所連続マルチンゲールである.一般に非負値局所連続マルチンゲールは優マルチンゲールであるから(KaratzasAndShreve, Problem1.5.19),証明が終わる.[証明終]
は非負値局所連続マルチンゲールである.一般に非負値局所連続マルチンゲールは優マルチンゲールであるから(KaratzasAndShreve, Problem1.5.19),証明が終わる.[証明終]
Xが単過程でないときは,Xを単過程でうまく近似して(KaratzasAndShreve, Problem3.2.27)Fatouの補題を使うことでも示せますが,準備が大変なので伊藤の公式をつかった証明で済ませました.また省略しましたが条件付き期待値のところで可測なものを外に出していますが,可積分性をチェックしなければいけません.それは 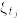 の有界性から従います.
の有界性から従います.
[追記] 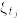 の有界性から議論するのではなく先に優マルチンゲールであることを言って
の有界性から議論するのではなく先に優マルチンゲールであることを言って
を言うのが早い気がしました.
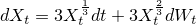
%7D%3D%5Cleft%5C%7B%0A%5Cbegin%7Barray%7D%7Bll%7D%0A0;%5Cquad%20%260%5Cleq%20t%3C%5Cbeta_%7B%5Ctheta%7D%5C%5C%0AW_t%5E3;%5Cquad%20%26%5Cbeta_%7B%5Ctheta%7D%5Cleq%20t%3C%5Cinfty%0A%5Cend%7Barray%7D%0A%5Cright..png)
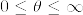
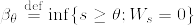
%7D.png)
%7D%3D0)%3D1.png)
%5E2%20%5C%7Dds%5Cbigg]%3D%5Cint_0%5EtE%5C%7B%20%7C3X_s%5E%7B%5Cfrac%7B1%7D%7B3%7D%7D%7C+(3X_s%5E%7B%5Cfrac%7B2%7D%7B3%7D%7D)%5E2%20%5C%7Dds%3C%5Cinfty%5Cquad%20(%5Cforall%7Bt%7D%5Cgeq%200,%20%7B%5Crm%20Fubini%7D).png)
%5E2%20%5C%7Dds%3C%5Cinfty%5Cbigg]%3D1.png)
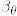
%7D%3D(W_t-W_%7Bt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D%7D)%5E3.png)
%7D%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7DW_t-W_%7Bt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D%7D.png)
%7D%3D(Z_t%5E%7B(%5Ctheta)%7D)%5E3%3D3%5Cint_0%5EtZ_s%5E%7B(%5Ctheta)%7Dd%5Clangle%20Z%5E%7B(%5Ctheta)%7D%5Crangle%20_s+3%5Cint_0%5Et(Z_s%5E%7B(%5Ctheta)%7D)%5E2dZ%5E%7B(%5Ctheta)%7D_s.png)
%7D_t%3D%5Cleft%5C%7B%0A%5Cbegin%7Barray%7D%7Bll%7D%0A0;%5Cquad%20%26(0%5Cleq%20t%3C%5Cbeta_%7B%5Ctheta%7D)%5C%5C%0AW_t;%5Cquad%20%26(%5Cbeta_%7B%5Ctheta%7D%5Cleq%20t%3C%5Cinfty)%0A%5Cend%7Barray%7D%0A%5Cright..png)
%7D%3D3%5Cint_0%5EtX_s%5E%7B(%5Ctheta)%7Dds+3%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E2dW_s.png)
%7D%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7DW_%7Bt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D%7D.png)
%7D)%5E%7B2/3%7DdZ_s%5E%7B(%5Ctheta)%7D%3D%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B2/3%7DdW_s-%5Cint_0%5Et%20(X_s%5E%7B(%5Ctheta)%7D)%5E%7B2/3%7DdA_s%5E%7B(%5Ctheta)%7D.png)
%7D)%5E%7B2/3%7DdA_s%5E%7B(%5Ctheta)%7D%5Cbigg)%5E2%5C%20%5Cbigg]%3DE%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B4/3%7Dd%5Clangle%20A%5E%7B(%5Ctheta)%7D%5Crangle_s.png)
%7D%5Crangle_t%3Dt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D.png)
%7D)%5E%7B4/3%7Dd%5Clangle%20A%5Crangle_s%5E%7B(%5Ctheta)%7D%5C%5C%0A%26%3D%26%5Cint_0%5E%7Bt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D%7D(X_s%5E%7B(%5Ctheta)%7D)%5E%7B4/3%7Dd%5Clangle%20A%5Crangle_s%5E%7B(%5Ctheta)%7D%3D0%5Cquad%20(X_t%5E%7B(%5Ctheta)%7D%3D0%5Cquad%200%5Cleq%20%5Cforall%7Bt%7D%5Cleq%20%5Cbeta_%7B%5Ctheta%7D).png)
%7D)%5E%7B1/3%7Dd%5Clangle%20Z%5E%7B(%5Ctheta)%7D_s%5C%5C%0A%26%3D%26%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B1/3%7Dds-2%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B1/3%7Dd%5Clangle%20W,A%5E%7B(%5Ctheta)%7D%5Crangle%20_s+%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B1/3%7Dd%5Clangle%20A%5E%7B(%5Ctheta)%7D%5Crangle_s.png)
%7D)%5E%7B1/3%7Dd%5Clangle%20A%5E%7B(%5Ctheta)%7D%5Crangle_s%3D0.png)
%7D)%5E%7B1/3%7Dd%5Clangle%20W,A%5E%7B(%5Ctheta)%7D%5Crangle%20_s%5Cbigg%7C%5Cleq%20%5Cbigg(%5Cint_0%5Et%20(X_s%5E%7B(%5Ctheta)%7D)%5E%7B2/3%7Dd%5Clangle%20A%5E%7B(%5Ctheta)%7D%5Crangle_s%5Cbigg)%5E%7B1/2%7D%5Cbigg(%5Cint_0%5Et1ds%5Cbigg)%5E%7B1/2%7D%3D0.png)
%3D%5Cbigg(%5Cfrac%7Bx%7D%7Br%7D%5Cbigg)%5E%7Bd-2%7D%5Cquad%20(0%5Cleq%20x%5Cleq%20r).png)
%7D%7C%5Cmathcal%7BF%7D_0]%3DM_%7B0%5Cwedge%20S_n%7D%5E%7B(n)%7D%3D1/r%5E%7Bd-2%7D%5Cquad%20%7B%5Crm%20a.s.%7D.png)
%7D%3DM_t%5E%7B(n)%7D1_%7B%5C%7BS_n%3D%5Cinfty%5C%7D%7D+M_%7Bt%5Cwedge%20S_n%7D%5E%7B(n)%7D1_%7B%5C%7B0%3CS_n%3C%5Cinfty%5C%7D%7D+M_0%5E%7B(n)%7D1_%7B%5C%7BS_n%3D0%5C%7D%7D.png)
%7D1_%7B%5C%7BS_n%3D%5Cinfty%5C%7D%7D%7C%5Cmathcal%7BF%7D_0]%3DE[M_%7BT_n%7D1_%7B%5C%7BS_n%3D%5Cinfty%5C%7D%7D%7C%5Cmathcal%7BF%7D_0].png)
%7D1_%7B%5C%7B0%3CS_n%3C%5Cinfty%5C%7D%7D%7C%5Cmathcal%7BF%7D_0]%3DE[M_%7BS_n%7D%5E%7B(n)%7D1_%7B%5C%7B0%3CS_n%3C%5Cinfty%5C%7D%7D%7C%5Cmathcal%7BF%7D_0].png)
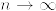
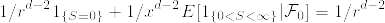
%3D1%5Cwedge%20(x/r)%5E%7Bd-2%7D.png)
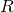
%3D1.png)

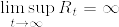
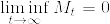
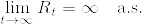
%5C%7D%7D.png)
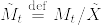
%3D1%5Cwedge%20%5Ctilde%7BM%7D_0.png)
%5C%7D%7D%7C%5Cmathcal%7BF%7D_0)%3D1%5Cwedge%20M_0/(X1_%7B%5C%7BX%5Cin(1/n,n)%5C%7D%7D).png)
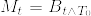
%3D1.png)
%3D1%5Cwedge%20a/x.png)
%3D1%5Cwedge%20a/x.png)
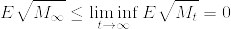
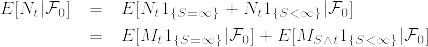


.png)
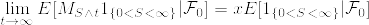

1_%7B%5C%7BS%3D0%5C%7D%7D+xP(M%5E*%5Cgeq%20x%7C%5Cmathcal%7BF%7D_0)%3DM_0.png)
%5Cgeq%20x.png)
%3D0.png)
+xP(M%5E*%5Cgeq%20x%7C%5Cmathcal%7BF%7D_0)%3DM_0.png)
%3D1.png)
%3DM_0.png)
%3DM_0/x.png)
%3D1%5Cwedge%20(M_0/x).png)
.png)
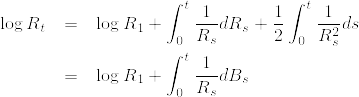
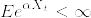
%5C%5C%0A%26%3D%26%5Cint_0%5E%5Cinfty%20%5Calpha%20y%5E%7B%5Calpha%20-1%7DP(1/R_t%3Ey)dy%20%5C%5C%0A%26%5Cleq%20%261+%5Cint_1%5E%7B%5Cinfty%7D%5Calpha%20y%5E%7B%5Calpha%20-1%7D%5Cfrac%7B1%7D%7B2%5Cpi%20t%7D%5Cfrac%7B%5Cpi%7D%7By%5E2%7Ddy%5C%5C%0A%26%3D%261+%5Cfrac%7B%5Calpha%20%7D%7B2t(2-%5Calpha%20)%7D%3C%5Cinfty%5Cquad%20%5Cforall%7Bt%7D%5Cgeq%201.png)
drd%5Ctheta%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B2t%7D%5Cint_0%5E%7B%5Cinfty%7Ds%5E%7B(%5Cbeta/2+1)-1%7D%5Cexp%20%5Cbigg(-%5Cfrac%7Bs%7D%7B2t%7D%5Cbigg)dr%5Cquad%20(s%3Dr%5E2)%5C%5C%0A%26%3D%26%5Cfrac%7B%5CGamma%20(%5Cbeta%20/2+1)%7D%7B(2t)%5E%7B%5Cbeta%20/2+2%7D%7D%3C%5Cinfty%0A.png)
%3C%5Cinfty%20%5Cquad%20(1%3C%5Cforall%7Bp%7D%3C2).png)
%26%3D%26%5Cint_0%5E%7B%5Cinfty%7Dpy%5E%7Bp-1%7DP(%7CX_t%7C%3Ey)dy%5C%5C%0A%26%5Cleq%20%26%5Cint_0%5E%7B%5Cinfty%7Dpy%5E%7Bp-1%7D%5Cexp(-py)E(%5Cexp(%7CpX_t%7C))dy%5C%5C%0A%26%5Cleq%20%26%20p(E(%5Cexp(pX_t))+E(%5Cexp(-pX_t))%5Cint_0%5E%7B%5Cinfty%7Dy%5E%7Bp-1%7D%5Cexp(-py)dy%5C%5C%0A%26%5Cleq%20%26%20p%5Cbigg(1+%5Cfrac%7Bp%7D%7B2t(2-p)%7D+%5Cfrac%7B%5CGamma%20(p/2+1)%7D%7B(2t)%5E%7Bp/2+2%7D%7D%5Cbigg)%5Cfrac%7B%5CGamma%20(p)%7D%7Bp%5Ep%7D%5C%5C%0A%26%5Cleq%20%26%20%5Cbigg(1+%5Cfrac%7Bp%7D%7B2(2-p)%7D+%5CGamma%20(p/2+1)%5Cbigg)%5Cfrac%7B%5CGamma%20(p)%7D%7Bp%5E%7Bp-1%7D%7D%3C%5Cinfty%20%5Cquad%20(t%5Cgeq%201).png)
%5C%5C%0A%26%3D%26%20%5Cint_%7B%5Ctheta%20%3D0%7D%5E%7B%5Ctheta%20%3D%202%5Cpi%7D%5Cint_%7Br%3D0%7D%5E%7Br%3D%5Cinfty%7D(-r%5Clog%20r)%5Cfrac%7B1%7D%7B2%5Cpi%20t%7D%5Cexp%20%5Cbigg(%20-%5Cfrac%7Br%5E2%7D%7B2t%7D%5Cbigg)drd%5Ctheta%5C%5C%0A%26%5Cleq%20%26%5Cfrac%7B1%7D%7Bte%7D%5Cint_%7B0%7D%5E%7B%5Cinfty%7D%5Cexp%5Cbigg(-%5Cfrac%7Br%5E2%7D%7B2t%7D%5Cbigg)dr%5C%5C%0A%26%3D%26%5Cfrac%7B%5Csqrt%7B2%5Cpi%7D%7D%7B2e%5Csqrt%7Bt%7D%7D.png)

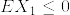

dr%5C%5C%0A%26%5Cgeq%20%26-%5Cint_0%5E%7B%5Cinfty%7Dr(r-1)%5Cexp(-r%5E2/2)dr%5C%5C%0A%26%3D%26-%5Cint_0%5E%7B%5Cinfty%7Dr%5E2%5Cexp(-r%5E2/2)dr+%5Cint_0%5E%7B%5Cinfty%7D%20r%5Cexp(-r%5E2/2)dr%5C%5C%0A%26%3D%26-%5Cfrac%7B1%7D%7B2%7D%5Cint_0%5E%7B%5Cinfty%7D%5Csqrt%7Bs%7D%5Cexp(-s/2)ds+1%5Cquad%20(s%3Dr%5E2)%5C%5C%0A%26%3D%26-%5Cfrac%7B%5CGamma%20(3/2)%7D%7B2%5E%7B3/2%7D%7D+1%5C%5C%0A%26%3D%26-%5Cfrac%7B%5Csqrt%7B%5Cpi%7D%7D%7B4%5Csqrt%7B2%7D%7D+1%3E0.png)
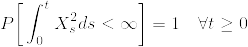
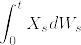
%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Cint_0%5Et%20X_sdW_s-%5Cfrac%7B1%7D%7B2%7D%5Cint_0%5EtX_s%5E2ds.png)
-%5Czeta_s(X))%7C%5Cmathcal%7BF%7D_s]%3D1%5Cquad%20%7B%5Crm%20a.s.%7D.png)
-%5Czeta_s(X))%3D%5Cexp%5Cbigg%5C%7B%5Csum_%7Bj%3D1%7D%5En%5Cbigg%5C%7B%5Cxi_%7Bt_j%7D(W_%7Bt_%7Bj+1%7D%7D-W_%7Bt_j%7D)-%5Cfrac%7B1%7D%7B2%7D%5Cxi_%7Bt_j%7D%5E2(t_%7Bj+1%7D-t_j)%20%5Cbigg%5C%7D%5Cbigg%5C%7D.png)

)%7C%5Cmathcal%7BF%7D_%7Bt_j%7D]%3D%5Cexp%5Cbigg(%5Cfrac%7B1%7D%7B2%7D%5Cxi_%7Bt_j%7D%5E2(t_%7Bj+1%7D-t_j)%5Cbigg).png)
)%7C%5Cmathcal%7BF%7D_s]%26%3D%26%5Cexp(%5Czeta_s(X))E[%5Cexp(%5Czeta_t(X)-%5Czeta_s(X))%7C%5Cmathcal%7BF%7D_s]%5C%5C%0A%26%3D%26%5Cexp(%5Czeta_s(X))%5Cquad%20%7B%5Crm%20a.s.%7D.png)
)%3D1+%5Cint_0%5Et%5Cexp(%5Czeta_s(X))X_sds.png)
)]%5Cleq%201.png)
-%5Czeta_s(X))]%5Cleq%20%5Csqrt%7BE[%5Cexp(2%5Czeta_t(X))]%7D%5Csqrt%7BE[%5Cexp(2%5Czeta_s(X))]%7D%5Cleq%201.png)