ゼータ分布に従う独立な確率変数が互いに素になる確率[D.Williams]
主張
X,Yは独立にゼータ分布に従うものとする.つまり
とする.このとき
(gcdは最大公約数)とすると,
となる.[D.Williams: Probability with martingales, p226]
証明
であるため.これより
となる.
次に.png) つまりX,Yが互いに疎になる確率を計算する.
つまりX,Yが互いに疎になる確率を計算する.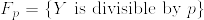 ,
,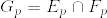 とすれば
とすれば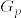 達は独立である.実際
達は独立である.実際
よりわかる.従って
\begin{eqnarray*}
P(H=1)
&=&P\bigg(\bigcap_{p:{\rm prime}}(E_p\cap F_p)^c\bigg)\\
&=&\prod_{p:{\rm prime}} P((E_p\cap F_p)^c)\\
&=&\prod_{p:{\rm prime}} (1-1/p^{2s})\\
&=&\frac{1}{\zeta(2s)}
\end{eqnarray*}
Xがpの倍数であるときのXの分布は,またゼータ分布になる:
nが素数でないときも
と定義すれば,条件付き期待値の性質から
となって示された.(包除原理を使って計算する方が正確だと思われます)[証明終]
ちなみにgcd(X,Y)の可測性は
から分かります.また結局互いに素な確率は
ということもわかり,面白いと思いました.
Hilbert--Schmidt作用素はコンパクト作用素
主張
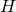 を可分なヒルベルト空間とし,
を可分なヒルベルト空間とし,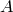 を
を 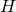 から
から 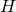 へのHilbert-Schmidt作用素とする.このとき
へのHilbert-Schmidt作用素とする.このとき 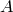 はコンパクト作用素である.
はコンパクト作用素である.
証明
事実1
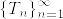 をコンパクト作用素とし,
をコンパクト作用素とし,
であるならば, 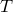 はコンパクトである(コンパクト作用素の全体はバナッハ空間なので).
はコンパクトである(コンパクト作用素の全体はバナッハ空間なので).
事実2
有界線形作用素の値域が有限次元空間であればコンパクトである(有限次元と局所コンパクトは同値).
この二つの事実を用います.
 を
を 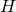 の内積とし,
の内積とし,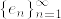 を完全正規直交系とする.有界線形作用素
を完全正規直交系とする.有界線形作用素 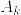 を
を
と定義する.事実2より 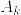 はコンパクト.
はコンパクト. 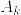 が
が 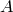 に強収束することを示せば,事実1より
に強収束することを示せば,事実1より 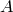 はコンパクトとなり,主張が示されたことになる.
はコンパクトとなり,主張が示されたことになる.
となる.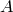 はHilbert-Schmidt作用素であるから,
はHilbert-Schmidt作用素であるから,
Hui-Hsiung Kuoの Gaussian Measures in Banach Spacesという本を読み始めました.上の主張はこの本のExerciseになっています.抽象ウィナー空間が分かるようになりたいです.
 | Gaussian Measures in Banach Spaces Hui-Hsiung Kuo 2006-06-29 売り上げランキング : 1234523 Amazonで詳しく見る by G-Tools |
Problem5.4.4
Problem5.4.4
連続で適合している確率過程 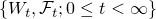 がd次元のブラウン運動であることの必要十分条件は
がd次元のブラウン運動であることの必要十分条件は
が任意の .png) に対して連続な局所マルチンゲールになることである.ただし
に対して連続な局所マルチンゲールになることである.ただし
とする.
証明
%7D,%5Cldots,%20W_t%5E%7B(d)%7D),%5Cmathcal%7BF%7D_t;0%5Cleq%20t%3C%5Cinfty%5C%7D.png) がd次元のブラウン運動であれば,
がd次元のブラウン運動であれば,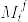 が連続な局所マルチンゲールであることは伊藤の公式から明らか(cf. Karatzas and Shreve, Proposition5.4.2, p312).逆に任意の
が連続な局所マルチンゲールであることは伊藤の公式から明らか(cf. Karatzas and Shreve, Proposition5.4.2, p312).逆に任意の .png) に対して
に対して 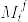 が連続な局所マルチンゲールになるとする.とくに
が連続な局所マルチンゲールになるとする.とくに %5Cmapsto%20x_i%5Cin%5Cmathbf%7BR%7D.png) について考えれば,
について考えれば,%7D-W_0%5E%7B(i)%7D.png) は連続な適合した局所マルチンゲールとなる.さらに
は連続な適合した局所マルチンゲールとなる.さらに 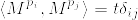 であることが,Karatzas and Shreve, Proposition5.4.2から分かる.よってLevy's characterization of Brownian motion よりこれらがd次元のブラウン運動であることがわかる.[証明終]
であることが,Karatzas and Shreve, Proposition5.4.2から分かる.よってLevy's characterization of Brownian motion よりこれらがd次元のブラウン運動であることがわかる.[証明終]
Problem5.3.13
Problem5.3.13
%5Cquad%20((t,x)%5Cin[0,%5Cinfty)%5Ctimes%20%5Cmathbf%7BR%7D%5Ed).png) はd×d行列で,任意の(t,x)に対して正則であるとする.また
はd×d行列で,任意の(t,x)に対して正則であるとする.また %5Cquad%20((t,x)%5Cin%20[0,%5Cinfty)%5Ctimes%20%5Cmathbf%7BR%7D%5Ed).png) は一様に有界であり,
は一様に有界であり,%5Csigma(t,x)%5E%7B%5Ctop%7D.png) の最小固有値は(t,x)によらずに下から正の値で抑えられているとする.さらに
の最小固有値は(t,x)によらずに下から正の値で抑えられているとする.さらに
は初期分布 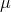 の弱解を持つとする.このとき確率微分方程式
の弱解を持つとする.このとき確率微分方程式
[証明]
まず %5E%7B-1%7Db(t,x)%5Cparallel%5E2%5Cquad%20(%5Cparallel%5Ccdot%5Cparallel:%7B%5Crm%20Euclidean%5C%20norm%7D).png) が(t,x)によらずに一様に上から抑えられることを示す.
が(t,x)によらずに一様に上から抑えられることを示す. %5Csigma(t,x)%5E%7B%5Ctop%7D.png) の固有ベクトルを正規直交基底として選び
の固有ベクトルを正規直交基底として選び ,a_2(t,x),%5Cldots,a_d(t,x).png) とし ,対応する固有値を
とし ,対応する固有値を %5Cleq%5Cldots%5Cleq%20%5Clambda_d(t,x).png) とする.ただしλは(t,x)によらない正の定数である.このとき,
とする.ただしλは(t,x)によらない正の定数である.このとき,
となるから
これより
これよりNovikovの条件からGirsanovの定理を用いて
は .png) の下でブラウン運動となる.よって
の下でブラウン運動となる.よって
(※)の等号は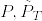 -a.s.で成立します.考えている確率空間が違いますが成立します(Karatzas and Shreve Problem3.5.6)
-a.s.で成立します.考えている確率空間が違いますが成立します(Karatzas and Shreve Problem3.5.6)
Exercise3.5.11(Robins&Siegmund(1973))
Exercise3.5.11
ν>0, c>1 に対して次のような 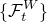 -stopping time を定義する.
-stopping time を定義する.
このとき
[証明]
より
あとは %7DR_c%3C%5Cinfty.png) であることを示せば十分である.なぜならばこれが成立すればWaldの恒等式から
であることを示せば十分である.なぜならばこれが成立すればWaldの恒等式から
となり,(1)の両辺の期待値をとって整理すれば
を得るからである.実際計算してみると
となり,証明が終わる.[証明終]
最後のR_cの可積分性を示すのに苦労しました.
Exercise3.5.10
Exercise3.5.10
Wをブラウン運動,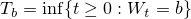 ,
, %7D.png) を前の記事と同じ確率測度とする.
を前の記事と同じ確率測度とする.%7D.png) を
を %7D.png) での期待値とすれば
での期待値とすれば
が成立する.
[証明]
あとは Exercise2.8.4 と同じように考えれば
λについての二次方程式 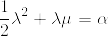 の解は
の解は 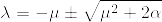 であり,
であり,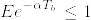 に注意してbの正負で場合分けしてλを選べば結論を得る.[証明終]
に注意してbの正負で場合分けしてλを選べば結論を得る.[証明終]
Problem3.5.7
Problem3.5.7
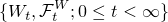 を一次元のブラウン運動とする.ただしフィルとレーションはWを可測にする最小のσ加法族とする.Tを
を一次元のブラウン運動とする.ただしフィルとレーションはWを可測にする最小のσ加法族とする.Tを.png) -stopping time でかつ,
-stopping time でかつ,%3D1.png) を満たすものとする.このときWaldの恒等式
を満たすものとする.このときWaldの恒等式
が成立することと,
として定義したものを 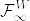 に一意的に拡張した測度である(Karatzas and Shreve, Corollary 3.5.2参照).
に一意的に拡張した測度である(Karatzas and Shreve, Corollary 3.5.2参照).
は上の条件を満たす.(Novikov conditionの証明に用いられる(Proposition 3.5.12))
[証明]
Optional Sampling Theoremから
よって単調収束定理から
特に, なら
なら  なので
なので %5Cleq%20P(S_b%3C%5Cinfty)%3D1.png) で
で %7D.png) のもとで,
のもとで,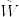 はブラウン運動になる(Girsanovの定理)ので
はブラウン運動になる(Girsanovの定理)ので
[証明終]
%3D%5Cfrac%7B1%7D%7Bn%5Es%5Czeta(s)%7D%20%5Cquad%20(%5Czeta(s):%3D%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7Bn%5Es%7D,s%3E1).png)
.png)
%3D%5Cfrac%7B1%7D%7Bn%5E%7B2s%7D%5Czeta(2s)%7D.png)
.png)
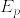
%26%3D%26%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7DP(X%3Dni_1%5Ccdots%20i_p)%5C%5C%0A%26%3D%26%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7B(ni_1%5Ccdots%20i_p)%5Es%5Czeta(s)%7D%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B(i_1%5Ccdots%20i_p)%5Es%7D.png)
%3D%5Cfrac%7B1%7D%7B(i_1%5Ccdots%20i_p)%5Es%7D.png)
%26%3D%26P(X%3D1)%5C%5C%0A%26%3D%26P%5Cbigg(%5Cbigcap_%7Bp:%7B%5Crm%20prime%7D%7DE_p%5Ec%5Cbigg)%5C%5C%0A%26%3D%26%5Cprod_%7Bp:%7B%5Crm%20prime%7D%7D(1-P(E_p))%5C%5C%0A%26%3D%26%5Cprod_%7Bp:%7B%5Crm%20prime%7D%7D(1-1/p%5Es).png)
%5C%5C%0A%26%3D%26P(E_%7Bi_1%7D%5Ccap%5Ccdots%20E_%7Bi_p%7D)P(F_%7Bi_1%7D%5Ccap%20%5Ccdots%20%5Ccap%20F_%7Bi_p%7D)%5Cquad%20(X,Y:%20%7B%5Crm%20independent%7D).png)
%3DP(X%3Dkp)/P(E_p)%3DP(X%3Dk).png)
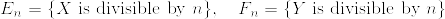
%26%3D%26P%5Cbigg(E_n%5Ccap%20F_n%5Ccap%20%5Cbigcap_%7Bp:%7B%5Crm%20prime%7D%7D(E_%7Bnp%7D%5Ccap%20F_%7Bnp%7D)%5Ec%20%5Cbigg)%5C%5C%0A%26%3D%26E%5Cbigg[1_%7BE_n%5Ccap%20F_n%7DP%5Cbigg(%5Cbigcap_%7Bp:%7B%5Crm%20prime%7D%7D(E_%7Bnp%7D%5Ccap%20F_%7Bnp%7D)%5Ec%7CE_n,F_n%5Cbigg)%5Cbigg]%5C%5C%0A%26%3D%26E[1_%7BE_n%7D1_%7BF_n%7DP(H%3D1)]%5C%5C%0A%26%3D%26n%5E%7B-2s%7D/%5Czeta(2s).png)
%3D%5Cprod_%7Bp:%7B%5Crm%20prime%7D%7D(p1_%7BE_p%7D1_%7BF_p%7D+%5Cmax%20%5C%7B1_%7BE_p%5Ec%7D,1_%7BF_p%5Ec%7D%5C%7D).png)
%3D1/%5Czeta(2s).png)
.png)
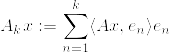
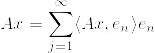
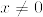
x%7C%5E2%26%3D%26%5Clim_%7BN%5Cto%5Cinfty%7D%5Csum_%7Bn%3Dk+1%7D%5E%7BN%7D%7C%5Clangle%20Ax,e_n%5Crangle%7C%5E2%5C%5C%0A%26%3D%26%5Clim_%7BN%5Cto%5Cinfty%7D%5Csum_%7Bn%3Dk+1%7D%5E%7BN%7D%7C%5Clangle%20x,A%5E*e_n%5Crangle%7C%5E2%5Cquad%20(A%5E*:%20%7B%5Crm%20adjoint~operator%7D)%5C%5C%0A%26%5Cleq%20%26%5Clim_%7BN%5Cto%5Cinfty%7D%7Cx%7C%5E2%5Csum_%7Bn%3Dk+1%7D%5E%7BN%7D%7CA%5E*e_n%7C%5E2%5C%5C%0A%26%3D%26%7Cx%7C%5E2%5Csum_%7Bn%3Dk+1%7D%5E%7B%5Cinfty%7D%7CA%5E*e_n%7C%5E2.png)
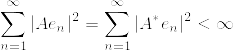
-f(W_0)-%5Cfrac%7B1%7D%7B2%7D%5Cint_0%5Et%5Cbigtriangleup%20f(W_s)ds,%5Cmathcal%7BF%7D_t;%5Cquad%200%5Cleq%20t%3C%5Cinfty.png)
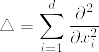
dW_t;%5Cquad%200%5Cleq%20t%5Cleq%20T%5Cquad%20(W:%7B%5Crm%20Brownian%5C%20motion%7D).png)
dt+%5Csigma(t,X_t)dW_t.png)
%3D%5Csum_%7Bj%3D1%7D%5Enc_j(t,x)a_j(t,x),%5Cquad%20%5Cparallel%20b(t,x)%5Cparallel%5E2%3D%5Csum_%7Bj%3D1%7D%5En%7Cc_j(t,x)%7C%5E2.png)
%5E%7B-1%7Db(t,x)%5Cparallel%5E2%5C%5C%0A%26%3D%26b(t,x)%5E%7B%5Ctop%7D(%5Csigma(t,x)%5Csigma(t,x)%5E%7B%5Ctop%7D)%5E%7B-1%7Db(t,x)%5C%5C%0A%26%3D%26%5Csum_%7Bi%3D1%7D%5En%5Csum_%7Bj%3D1%7D%5Enc_i(t,x)c_j(t,x)a_i(t,x)(%5Csigma(t,x)%5Csigma(t,x)%5E%7B%5Ctop%7D)%5E%7B-1%7Da_j(t,x)%5C%5C%0A%26%3D%26%5Csum_%7Bi%3D1%7D%5En%5Csum_%7Bj%3D1%7D%5En%5Cfrac%7Bc_i(t,x)c_j(t,x)%7D%7B%5Clambda_j(t,x)%7Da_i(t,x)a_j(t,x)%5C%5C%0A%26%3D%26%5Csum_%7Bi%3D1%7D%5En%5Cfrac%7Bc_i(t,x)%5E2%7D%7B%5Clambda_i(t,x)%7D%5Cquad%20(%5C%7Ba_i(t,x)%5C%7D:%7B%5Crm%20orthonormal%5C%20basis%7D)%5C%5C%0A%26%5Cleq%20%26%5Cfrac%7B1%7D%7B%5Clambda%7D%5Cparallel%20b(t,x)%5Cparallel%5E2%5C%5C%0A%26%5Cleq%20%26M%5Cquad%20(M:%7B%5Crm%20const%7D,%5Cquad%20b(t,x):%7B%5Crm%20uniformly%5C%20bounded%7D).png)
,(%5COmega,%5Cmathcal%7BF%7D,P),%5C%7B%5Cmathcal%7BF%7D_t%5C%7D.png)
%5E%7B-1%7Db(s,X_s)%5Cparallel%5E2ds%5Cbigg)%5Cbigg]%26%5Cleq%26%5Cexp(Mt/2)%5C%5C%0A%26%3C%26%5Cinfty%20%5Cquad%20(0%5Cleq%20t%3C%5Cinfty).png)
%5E%7B-1%7Db(s,X_s)ds%5Cquad%20(0%5Cleq%20t%5Cleq%20T).png)
dW_s%3D%5Cint_0%5Etb(s,X_s)ds+%5Cint_0%5Et%5Csigma(s,X_s)d%5Ctilde%7BW%7D_s.png)
,(%5COmega,%5Cmathcal%7BF%7D_T,%5Ctilde%7BP%7D_T),%5C%7B%5Cmathcal%7BF%7D_t%5C%7D.png)
%3Dc%5C%7D.png)
%7DR_c%3D%5Cfrac%7B2%5Clog%20c%7D%7B%5Cnu%5E2%7D..png)
)%5C%5C%0A%26%3D%26%5Clim_%7Bt%5Cto%5Cinfty%7DE[1_%7B%5C%7BR_c%5Cleq%20t%5C%7D%7DZ_%7BR_c%7D]%5Cquad%20(%7B%5Crm%20by%5C%20the%5C%20monotone%5C%20convergence%5C%20thoerem%7D)%5C%5C%0A%26%3D%26%5Clim_%7Bt%5Cto%5Cinfty%7DE[1_%7B%5C%7BR_c%5Cleq%20t%5C%7D%7DZ_%7BR_c%5Cwedge%20t%7D]%5C%5C%0A%26%3D%26%5Clim_%7Bt%5Cto%5Cinfty%7DE[1_%7B%5C%7BR_c%5Cleq%20t%5C%7D%7DE[Z_t%7C%5Cmathcal%7BF%7D_%7Bt%5Cwedge%20R_c%7D]]%5Cquad%20(%7B%5Crm%20by%5C%20the%5C%20optional%5C%20sampling%5C%20theorem%7D)%5C%5C%0A%26%3D%26%5Clim_%7Bt%5Cto%5Cinfty%7DE[E[1_%7B%5C%7BR_c%5Cleq%20t%5C%7D%7DZ_t%7C%5Cmathcal%7BF%7D_%7Bt%5Cwedge%20R_c%7D]]%5C%5C%0A%26%3D%26%5Clim_%7Bt%5Cto%5Cinfty%7DE[1_%7B%5C%7BR_c%5Cleq%20t%5C%7D%7DZ_t]%5C%5C%0A%26%3D%26%5Clim_%7Bt%5Cto%5Cinfty%7D(EZ_t-E[1_%7B%5C%7BR_c%3E%20t%5C%7D%7DZ_t])%5C%5C%0A%26%3D%261%5Cquad%20(%7B%5Crm%20by%5C%20the%5C%20Lebesgue%5C%20convergence%5C%20theorem%7D).png)
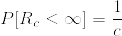
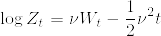
.png)
%7DW_%7BR_c%7D%3DE%5E%7B(%5Cnu)%7D%5Ctilde%7BW%7D_%7BR_c%7D+%5Cnu%20E%5E%7B(%5Cnu)%7DR_c%3D%5Cnu%20E%5E%7B(%5Cnu)%7DR_c.png)
%7DR_c%3D%5Cfrac%7B2%5Clog%20c%7D%7B%5Cnu%5E2%7D.png)
%7DR_c%26%3D%26%5Cint_0%5E%7B%5Cinfty%7DP%5E%7B(%5Cnu)%7D[R_c%5Cgeq%20t]dt%5C%5C%0A%26%5Cleq%26%5Cint_0%5E%7B(4%5Clog%20c)/%5Cnu%5E2%7DP%5E%7B(%5Cnu)%7D[R_c%5Cgeq%20t]dt+%5Cint_%7B(4%5Clog%20c)/%5Cnu%5E2%7D%5E%7B%5Cinfty%7DP%5E%7B(%5Cnu)%7D[R_c%5Cgeq%20t]dt%5C%5C%0A%26%5Cleq%20%26(4%5Clog%20c)/%5Cnu%5E2+%5Cint_%7B(4%5Clog%20c)/%5Cnu%5E2%7D%5E%7B%5Cinfty%7DP%5E%7B(%5Cnu)%7D[%5Ctilde%7BW%7D_t%5Cleq%20-%5Cnu%20t/4]dt%5C%5C%0A%26%5Cleq%20%26(4%5Clog%20c)/%5Cnu%5E2%20+%20%5Cint_0%5E%7B%5Cinfty%7D%5Cbigg(%5Cint_%7B-%5Cinfty%7D%5E%7B-%5Cnu%20t/4%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%20t%7D%7D%5Cexp(-%5Cfrac%7Bx%5E2%7D%7B2t%7D)%5Cbigg)dt%5C%5C%0A%26%3D%26(4%5Clog%20c)/%5Cnu%5E2%20+%20%5Cint_0%5E%7B%5Cinfty%7D%5Cbigg(%5Cint_%7B%5Cnu%20%5Csqrt%7Bt%7D/4%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%7D%5Cexp(-%5Cfrac%7Bu%5E2%7D%7B2%7D)%5Cbigg)dt%5C%5C%0A%26%5Cleq%20%26(4%5Clog%20c)/%5Cnu%5E2%20+%20%5Cint_0%5E%7B%5Cinfty%7D%5Cfrac%7B4%7D%7B%5Cnu%5Csqrt%7Bt%7D%7D%5Cexp(-%5Cnu%5E2t/32)dt%5C%5C%0A%26%3D%26(4%5Clog%20c)/%5Cnu%5E2%20+%5Cfrac%7B4%7D%7B%5Cnu%7D%5CGamma(3/2)(%5Cnu%5E2/32)%5E%7B-3/2%7D%3C%5Cinfty.png)
%7De%5E%7B-%5Calpha%20T_b%7D%3D%5Cexp%20(%5Cmu%20b-%7Cb%7C%5Csqrt%7B%5Cmu%5E2%20+2%5Calpha%7D).png)
%7D[%5Ctilde%7BX%7D_t]%5Cquad%20(0%5Cleq%20t%3C%5Cinfty)%5C%5C%0A%26%3D%26E%5E%7B(%5Cmu)%7D[E%5E%7B(%5Cmu)%7D[%5Ctilde%7BX%7D_t%7C%5Cmathcal%7BF%7D%5EW_%7Bt%5Cwedge%20T_b%7D]]%5C%5C%0A%26%3D%26E%5E%7B(%5Cmu)%7D[1_%7B%5C%7BT_b%3Et%5C%7D%7D%5Ctilde%7BX%7D_t]+E%5E%7B(%5Cmu)%7D[1_%7B%5C%7BT_b%5Cleq%20t%5C%7D%7D%5Ctilde%7BX%7D_%7BT_b%7D].png)
1_%7B%5C%7BT_b%3C%5Cinfty%5C%7D%7D]%3D1.png)
]%3D1.png)
%7D(T%3C%5Cinfty)%3D1.png)
%5Cquad%20(%5Cmu%5Cneq%200).png)
%7D(A)%3DE[1_AZ_t];%5Cquad%20A%5Cin%20%5Cmathcal%7BF%7D_t%5EW.png)
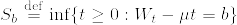
%7D[T%5Cleq%20t]%5Cquad%20(0%5Cleq%20t%3C%5Cinfty)%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DZ_t]%20%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DE[Z_t%7C%5Cmathcal%7BF%7D_%7Bt%5Cwedge%20T%7D]]%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DZ_%7Bt%5Cwedge%20T%7D]%5C%5C%0A%26%3D%26E[1_%7B%5C%7BT%5Cleq%20t%5C%7D%7DZ_T].png)
%7D(T%3C%5Cinfty)%3DE[Z_T]%3DE[%5Cexp%20(%5Cmu%20W_T-%5Cfrac%7B1%7D%7B2%7D%5Cmu%20%5E2%20T)].png)
%7D(S_b%3C%5Cinfty)%3DP%5E%7B(%5Cmu)%7D(%5Cinf%5C%7Bt%5Cgeq%200:%5Ctilde%7BW%7D_t%3Db%5C%7D)%3D1.png)