multicore (R)
Rのライブラリ multicore を試した結果です.
mclappy()という関数を使いました.
この関数は lapply() を並列でできるようにしたもので,
独立に繰り返し計算する必要がある場合(乱数や初期値を変えた結果が欲しいときなど)
に簡単に並列で計算できます.
例えば k-means 法を R で行う場合に kmeans() という関数があります.
この関数は
kmeans(x, centers, iter.max = 10, nstart = 1, algorithm = c("Hartigan-Wong", "Lloyd", "Forgy", "MacQueen"))
という形になっていて,x としてクラスタリングしたいデータ,centers に
クラスタ数をとります.このときクラスターの初期値を nstart 回ランダムに選び,
その結果もっともクラスター内平方和(tot.withinss)を小さくした結果を返します.
k-meansの各初期値からの反復は,ほかの初期値を選んだ場合の結果に依存しないので
簡単に並列化できると考えられます.
そこで並列で計算させた場合にどれくらい早くなるか実験しました.
まず mclapply() は
mclapply(X, FUN, ..., mc.preschedule = TRUE, mc.set.seed = TRUE, mc.silent = FALSE, mc.cores = 1L, mc.cleanup = TRUE, mc.allow.recursive = TRUE)
となっています.
lapply() と同じで,X の要素に関数 FUN を作用させた結果をリストで返します.
mc.cores が(最大限)使うコアの数です.
これを踏まえ,ライブラリMASSにあるデータ Boston を4つのクラスタに k-means 法を使ってクラスタリングしました.
初期値は 5000*n 個 (n=1,2,...,10) 与え,並列したときとかかった時間の差を調べました.
並列させないときは
t <- proc.time() invisible(kmeans(Boston, 4, nstart=5000*n)) duration <- (proc.time() - t)[3]
で時間を計り,並列させたときは
t <- proc.time() results <- mclapply(rep(5000*n/8, 8), function(nstart) kmeans(Boston, 4, nstart=nstart)) #collect results objective.values <- sapply(results, function(result) result$tot.withinss) result.best <- results[[which.min(objective.values)]] duration <- (proc.time() - t)[3]
で時間を計りました.
#collect results の後の二行はクラスター内平方和(tot.withinss)を小さくした結果を返すための部分です.
mclapply() は mc.cores を指定しないと,自動で使えるコアの数を調べます.
自分が実験した環境だとコアの数が8だったので,5000*n個の初期値を
8個に分割しています.分割数に差があるかどうかを調べるために
9個に分割した場合も調べました:
t <- proc.time() results <- mclapply(rep(5000*n/9, 9), function(nstart) kmeans(Boston, 4, nstart=nstart)) objective.values <- sapply(results, function(result) result$tot.withinss) result.best <- results[[which.min(objective.values)]] duration <- (proc.time() - t)[3]
細かいですが kmeans() は nstart の値が小数でもエラーがでず,nstartの小数以下を切り捨てた回数だけ初期値をランダムに発生させて計算しています(1:4.5と1:4が同じため).
結果としては次のようになりました:

横軸は初期値の数(5000*n),縦軸はかかった時間です.
凡例の cores の値は使ったコアの数で,list の値は 5000*n 個の初期値の分割数です.
コア数が多い方が当然早く計算ができることが分かりました.
また初期値の分割数はコア数の倍数にした方がいいと思われます.
実際 multicore のマニュアルを読むと
"By default (mc.preschedule=TRUE) the input vector/list X is split into as many parts as there are cores (currently the values are spread across the cores sequentially, i.e. first value to core 1, second to core 2, ... (core + 1)-th value to core 1 etc.) and then one process is spawned to each core and the results are collected."
とあります.そこでコア数の倍数である16, 24分割した場合は8分割の場合とほとんど同じ結果になりました(凡例の一番上はcores=8の間違いです):

以上をまとめると
・並列計算したほうが早く,multicoreのmclapply()で簡単にできる
・初期値や乱数の分割はコア数の倍数にした方が良い(一つ一つの計算量が同じなら)
snowとかも調べてみたいと思います.
Contiguity
統計にでてくるContiguityの概念についての問題(van der Vaart: Asymptotic Statistics. Chap 6.)を解いたので,そのまとめです.
問題
(1) 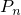 を標準正規分布,
を標準正規分布,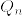 を平均
を平均 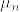 分散1の正規分布とする.このとき
分散1の正規分布とする.このとき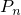 と
と 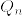 が互いにcontiguousであることと,
が互いにcontiguousであることと,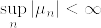 は同値であることを示せ.
は同値であることを示せ.
(2) total variation を
とすると
(3) 任意の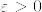 に対して,
に対して,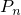 と
と 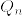 は互いにcontiguousであるが,
は互いにcontiguousであるが,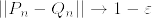 となる例を見つけよ.
となる例を見つけよ.
(4) 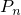 は
は 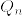 に対してcontiguousであるが,
に対してcontiguousであるが,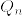 は
は 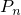 に対してcontiguousでない例を挙げよ.
に対してcontiguousでない例を挙げよ.
(5) 二つの確率測度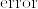 ,
,  が互いに絶対連続であることと,確率測度の列
が互いに絶対連続であることと,確率測度の列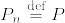 ,
, 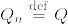 が互いにcontiguousであることは同値である.
が互いにcontiguousであることは同値である.
証明
(1) 互いにcontiguousなら,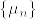 が有界であることを対偶を使って示す.
が有界であることを対偶を使って示す.
とする.このとき 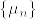 の部分列で
の部分列で 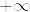 または
または 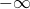 となるものが存在する.この部分列を
となるものが存在する.この部分列を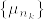 とし,
とし,
とすると,
より互いにcontiguousでない.よって互いにcontiguousなら,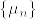 が有界である.
が有界である.
逆を示す.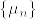 が有界であるとする.
が有界であるとする.%3D0.png) とする.
とする.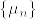 が有界であるから,任意の
が有界であるから,任意の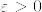 に対して,ある
に対して,ある があって,
があって,
となる(tight).このとき
となるから,
よって 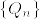 は
は 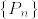 に対してcontiguous.同様に
に対してcontiguous.同様に 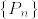 は
は 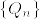 に対してcontiguousであることが分かる.よって同値性が示された.
に対してcontiguousであることが分かる.よって同値性が示された.
(2) %3D0.png) とする.total variationが0に収束するという仮定より,任意の
とする.total variationが0に収束するという仮定より,任意の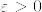 に対して,ある
に対して,ある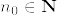 があって,
があって,
よって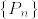 は
は 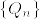 に対してcontiguousであることが示された.条件の対称性から同様にして,互いにcontiguousであることが分かる.
に対してcontiguousであることが示された.条件の対称性から同様にして,互いにcontiguousであることが分かる.
(3) 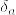 を
を  に台を持つディラック測度とする.
に台を持つディラック測度とする.
とすれば互いにcontiguousであるが,total variation は集合{0}のときに となる.
となる.
(4)
とすれば条件を満たす.
(5) 二つの確率測度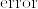 ,
, 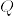 が互いに絶対連続であるとする.このときラドン--ニコディム微分
が互いに絶対連続であるとする.このときラドン--ニコディム微分
はそれぞれの確率測度の下で可積分である.
であるから,
よって 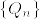 は
は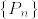 に対してcontiguousである.全く同様にして
に対してcontiguousである.全く同様にして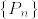 は
は 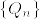 に対してcontiguousである.
に対してcontiguousである.
次に確率測度の列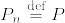 ,
, 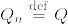 が互いにcontiguousであるとする.
が互いにcontiguousであるとする.%3D0.png) とする.
とする.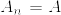 とすれば,contiguityより
とすれば,contiguityより%3DQ(A)%3D0.png) .よってQはPに関して絶対連続.同様にPはQに関して絶対連続.[証明終]
.よってQはPに関して絶対連続.同様にPはQに関して絶対連続.[証明終]
Ostrowski-Taussky Inequality
Ostrowski-Taussky Inequality
Aを正方行列とし,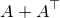 が正定値行列であるとする.このとき以下の不等式が成立する:
が正定値行列であるとする.このとき以下の不等式が成立する:
となっている.このような行列に関して次の不等式が成立する(下の補第参照):
これが成り立てば
これより証明が終わる.あとは次の補題1を示せばよい.ただし帰納法の成立のため主張を拡張する.
補第1
証明
Bの次元に関する帰納法で示す.n=1のときは明らかに成立する.n=k-1のとき成立するとする.まず次のように行列Bを分割する.
ここでCは(k-1)×(k-1)行列である.まず任意の%5E%7B%5Ctop%7D%5Cin%5Cmathbf%7BR%7D%5En.png) に対して,
に対して,%5E%7B%5Ctop%7D.png) として,
として,
となることがまずわかる.
次に, よりブロック行列の行列式を考えれば
よりブロック行列の行列式を考えれば
帰納法の仮定からCは正則であるから,Sherman-Morrison-Woodburyの公式より
ここで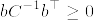 であることがわかる.実際帰納法の仮定より
であることがわかる.実際帰納法の仮定より
Cは正則だから任意のxに対してあるyがあって
よって任意のxに対して
となるためである.これより
[証明終]
主張が言いたいことを考えると,これは複素数zに対する不等式
の行列への拡張ではないかという指摘を受けました.というのも
と分けます.右辺の第一項はAを対称化したもので,第二項は反対称化したものです.実対称行列の固有値は実数で,反対称行列の固有値は純虚数です.つまり固有値の視点から見ると,上の分解は行列の実部と虚部への分解に対応するものではないかと考えられます.そうすると主張の左辺はAの固有値の実部の積,右辺は固有値の絶対値の積なので,不等号が成り立つと思われます.これを正当化するには,右辺の第一項と第二項が同時三角化可能で,行列の和の固有値が,各行列の固有値の和になることを言わないとダメだと思いますが...
ちなみに主張の右辺の絶対値は要らないことが証明から分かります.
ゼータ分布に従う独立な確率変数が互いに素になる確率[D.Williams]
主張
X,Yは独立にゼータ分布に従うものとする.つまり
とする.このとき
(gcdは最大公約数)とすると,
となる.[D.Williams: Probability with martingales, p226]
証明
であるため.これより
となる.
次に.png) つまりX,Yが互いに疎になる確率を計算する.
つまりX,Yが互いに疎になる確率を計算する.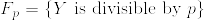 ,
, とすれば
とすれば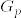 達は独立である.実際
達は独立である.実際
よりわかる.従って
\begin{eqnarray*}
P(H=1)
&=&P\bigg(\bigcap_{p:{\rm prime}}(E_p\cap F_p)^c\bigg)\\
&=&\prod_{p:{\rm prime}} P((E_p\cap F_p)^c)\\
&=&\prod_{p:{\rm prime}} (1-1/p^{2s})\\
&=&\frac{1}{\zeta(2s)}
\end{eqnarray*}
Xがpの倍数であるときのXの分布は,またゼータ分布になる:
nが素数でないときも
と定義すれば,条件付き期待値の性質から
となって示された.(包除原理を使って計算する方が正確だと思われます)[証明終]
ちなみにgcd(X,Y)の可測性は
から分かります.また結局互いに素な確率は
ということもわかり,面白いと思いました.
Hilbert--Schmidt作用素はコンパクト作用素
主張
 を可分なヒルベルト空間とし,
を可分なヒルベルト空間とし,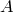 を
を  から
から  へのHilbert-Schmidt作用素とする.このとき
へのHilbert-Schmidt作用素とする.このとき 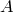 はコンパクト作用素である.
はコンパクト作用素である.
証明
事実1
 をコンパクト作用素とし,
をコンパクト作用素とし,
であるならば, 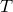 はコンパクトである(コンパクト作用素の全体はバナッハ空間なので).
はコンパクトである(コンパクト作用素の全体はバナッハ空間なので).
事実2
有界線形作用素の値域が有限次元空間であればコンパクトである(有限次元と局所コンパクトは同値).
この二つの事実を用います.
 を
を  の内積とし,
の内積とし,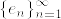 を完全正規直交系とする.有界線形作用素
を完全正規直交系とする.有界線形作用素  を
を
と定義する.事実2より  はコンパクト.
はコンパクト.  が
が  に強収束することを示せば,事実1より
に強収束することを示せば,事実1より  はコンパクトとなり,主張が示されたことになる.
はコンパクトとなり,主張が示されたことになる.
となる. はHilbert-Schmidt作用素であるから,
はHilbert-Schmidt作用素であるから,
Hui-Hsiung Kuoの Gaussian Measures in Banach Spacesという本を読み始めました.上の主張はこの本のExerciseになっています.抽象ウィナー空間が分かるようになりたいです.
 | Gaussian Measures in Banach Spaces Hui-Hsiung Kuo 2006-06-29 売り上げランキング : 1234523 Amazonで詳しく見る by G-Tools |
Problem5.4.4
Problem5.4.4
連続で適合している確率過程 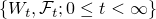 がd次元のブラウン運動であることの必要十分条件は
がd次元のブラウン運動であることの必要十分条件は
が任意の .png) に対して連続な局所マルチンゲールになることである.ただし
に対して連続な局所マルチンゲールになることである.ただし
とする.
証明
%7D,%5Cldots,%20W_t%5E%7B(d)%7D),%5Cmathcal%7BF%7D_t;0%5Cleq%20t%3C%5Cinfty%5C%7D.png) がd次元のブラウン運動であれば,
がd次元のブラウン運動であれば,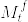 が連続な局所マルチンゲールであることは伊藤の公式から明らか(cf. Karatzas and Shreve, Proposition5.4.2, p312).逆に任意の
が連続な局所マルチンゲールであることは伊藤の公式から明らか(cf. Karatzas and Shreve, Proposition5.4.2, p312).逆に任意の .png) に対して
に対して 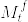 が連続な局所マルチンゲールになるとする.とくに
が連続な局所マルチンゲールになるとする.とくに %5Cmapsto%20x_i%5Cin%5Cmathbf%7BR%7D.png) について考えれば,
について考えれば,%7D-W_0%5E%7B(i)%7D.png) は連続な適合した局所マルチンゲールとなる.さらに
は連続な適合した局所マルチンゲールとなる.さらに 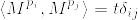 であることが,Karatzas and Shreve, Proposition5.4.2から分かる.よってLevy's characterization of Brownian motion よりこれらがd次元のブラウン運動であることがわかる.[証明終]
であることが,Karatzas and Shreve, Proposition5.4.2から分かる.よってLevy's characterization of Brownian motion よりこれらがd次元のブラウン運動であることがわかる.[証明終]
Problem5.3.13
Problem5.3.13
%5Cquad%20((t,x)%5Cin[0,%5Cinfty)%5Ctimes%20%5Cmathbf%7BR%7D%5Ed).png) はd×d行列で,任意の(t,x)に対して正則であるとする.また
はd×d行列で,任意の(t,x)に対して正則であるとする.また %5Cquad%20((t,x)%5Cin%20[0,%5Cinfty)%5Ctimes%20%5Cmathbf%7BR%7D%5Ed).png) は一様に有界であり,
は一様に有界であり,%5Csigma(t,x)%5E%7B%5Ctop%7D.png) の最小固有値は(t,x)によらずに下から正の値で抑えられているとする.さらに
の最小固有値は(t,x)によらずに下から正の値で抑えられているとする.さらに
は初期分布 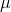 の弱解を持つとする.このとき確率微分方程式
の弱解を持つとする.このとき確率微分方程式
[証明]
まず %5E%7B-1%7Db(t,x)%5Cparallel%5E2%5Cquad%20(%5Cparallel%5Ccdot%5Cparallel:%7B%5Crm%20Euclidean%5C%20norm%7D).png) が(t,x)によらずに一様に上から抑えられることを示す.
が(t,x)によらずに一様に上から抑えられることを示す. %5Csigma(t,x)%5E%7B%5Ctop%7D.png) の固有ベクトルを正規直交基底として選び
の固有ベクトルを正規直交基底として選び ,a_2(t,x),%5Cldots,a_d(t,x).png) とし ,対応する固有値を
とし ,対応する固有値を %5Cleq%5Cldots%5Cleq%20%5Clambda_d(t,x).png) とする.ただしλは(t,x)によらない正の定数である.このとき,
とする.ただしλは(t,x)によらない正の定数である.このとき,
となるから
これより
これよりNovikovの条件からGirsanovの定理を用いて
は .png) の下でブラウン運動となる.よって
の下でブラウン運動となる.よって
(※)の等号は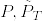 -a.s.で成立します.考えている確率空間が違いますが成立します(Karatzas and Shreve Problem3.5.6)
-a.s.で成立します.考えている確率空間が違いますが成立します(Karatzas and Shreve Problem3.5.6)
-Q(A)%7C.png)
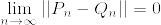
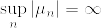
%5C%5C%0A(%5Cmu_%7Bn_k%7D,%5Cinfty)%20%20%26%20(n%3Dn_k,%20%5Cmu_%7Bn_k%7D%5Cgeq%200)%5C%5C%0A(n,%5Cinfty)%20%26%20(n%5Cneq%20n_k)%5C%5C%0A%5Cend%7Barray%7D%0A%5Cright..png)
%3D0,%5Cquad%20%5Climsup_%7Bn%7DQ_n(A_n)%5Cgeq%201/2.png)
%3C%5Cvarepsilon.png)
%26%3D%26%5Cint_%7B%5Cmathbf%7BR%7D%7D1_%7BA_n%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%7D%5Cexp%5Cbigg(-%5Cfrac%7B(x-%5Cmu_n)%5E2%7D%7B2%7D%5Cbigg)%7B%5Crm%20d%7Dx%5C%5C%0A%26%3D%26%5Cint_%7B%7Cx%7C%3EM%7D%20+%20%5Cint_%7B%7Cx%7C%5Cleq%20M%7D%5C%5C%0A%26%3C%20%26%5Cvarepsilon%20+%20%5Cint_%7B%7Cx%7C%5Cleq%20M%7D1_%7BA_n%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%7D%5Cexp%5Cbigg(-%5Cfrac%7Bx%5E2%7D%7B2%7D%5Cbigg)%5Cexp%5Cbigg(%5Cmu_n%20x-%5Cfrac%7B%5Cmu_n%5E2%7D%7B2%7D%5Cbigg)%7B%5Crm%20d%7Dx%5C%5C%0A%26%5Cleq%20%26%5Cvarepsilon%20+%20%5Cexp(CM)P_n(A_n)%5Cquad%20(C%3D%5Csup_n%7C%5Cmu_n%7C,%20%5Cexp(-%5Cmu_n%5E2/2)%5Cleq%201).png)
%5Cleq%20%5Cvarepsilon.png)
%3C%5Cvarepsilon/2..png)

%3D(P_n(A_n)-Q_n(A_n))+Q_n(A_n)%5Cleq%20%7C%7CP_n-Q_n%7C%7C+Q_n(A_n)%3C%5Cvarepsilon.png)
%5Cdelta_0+%5Cfrac%7B%5Cvarepsilon%7D%7B2%7D%5Cdelta_1.png)
%5Cdelta_1.png)
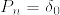
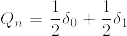
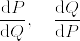
%3D0%5CRightarrow%20%5Clim_n%201_%7BA_n%7D%3D0%20%5Cquad%20P-%7B%5Crm%20a.s.%7D%0A.png)
%3D%5Cint%201_%7BA_n%7D%5Cfrac%7B%7B%5Crm%20d%7DQ%7D%7B%7B%5Crm%20d%7DP%7D%7B%5Crm%20d%7DP%5Cto%20%5Cint%200%5Ccdot%20%5Cfrac%7B%7B%5Crm%20d%7DQ%7D%7B%7B%5Crm%20d%7DP%7D%7B%5Crm%20d%7DP%3D0%5C%5C(%7B%5Crm%20Lebesgue's%20%5C%20convergence%5C%20%20theorem.%7D).png)
%5Cleq%20%7C%5Cdet(A)%7C..png)
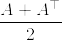
P%3D%7B%5Crm%20diag%7D[%5Clambda_1,%5Cldots,%5Clambda_n],%5Cquad%20%5Clambda_i%3E0~(i%3D1,2,%5Cldots,n).png)
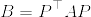
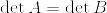
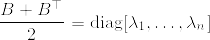
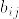
%5C%5C%0A-b_%7Bji%7D%20%26%20(i%5Cneq%20j)%0A%5Cend%7Barray%7D%0A%5Cright..png)

%26%3D%26%5Cdet(%7B%5Crm%20diag%7D[%5Clambda_1,%5Cldots,%5Clambda_n])%5C%5C%0A%26%3D%26%5Cprod_%7Bi%3D1%7D%5En%5Clambda_i%5C%5C%0A%26%5Cleq%20%26%5Cdet%20B%5C%5C%0A%26%3D%26%5Cdet%20A..png)
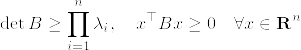
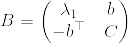
%5E2+(%5Chat%7Bx%7D%5E%7B%5Ctop%7DC%5Chat%7Bx%7D)%5Cgeq%200.png)
..png)
%3D%5Clambda_1(1+bC%5E%7B-1%7Db%5E%7B%5Ctop%7D)%5Cdet%20C%5C%5C%0A.png)
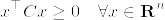
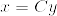
%5E%7B%5Ctop%7D%5C%5C%0A%26%3D%26y%5E%7B%5Ctop%7DCy%5Cgeq%200.png)
%5Cdet%20C%5C%5C%0A%26%5Cgeq%20%26%5Clambda_1%5Cdet%20C%5C%5C%0A%26%5Cgeq%20%26%5Cprod_%7Bi%3D1%7D%5En%5Clambda_i..png)
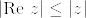
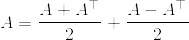
%3D%5Cfrac%7B1%7D%7Bn%5Es%5Czeta(s)%7D%20%5Cquad%20(%5Czeta(s):%3D%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7Bn%5Es%7D,s%3E1).png)
.png)
%3D%5Cfrac%7B1%7D%7Bn%5E%7B2s%7D%5Czeta(2s)%7D.png)
.png)
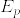
%26%3D%26%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7DP(X%3Dni_1%5Ccdots%20i_p)%5C%5C%0A%26%3D%26%5Csum_%7Bn%3D1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7B(ni_1%5Ccdots%20i_p)%5Es%5Czeta(s)%7D%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B(i_1%5Ccdots%20i_p)%5Es%7D.png)
%3D%5Cfrac%7B1%7D%7B(i_1%5Ccdots%20i_p)%5Es%7D.png)
%26%3D%26P(X%3D1)%5C%5C%0A%26%3D%26P%5Cbigg(%5Cbigcap_%7Bp:%7B%5Crm%20prime%7D%7DE_p%5Ec%5Cbigg)%5C%5C%0A%26%3D%26%5Cprod_%7Bp:%7B%5Crm%20prime%7D%7D(1-P(E_p))%5C%5C%0A%26%3D%26%5Cprod_%7Bp:%7B%5Crm%20prime%7D%7D(1-1/p%5Es).png)
%5C%5C%0A%26%3D%26P(E_%7Bi_1%7D%5Ccap%5Ccdots%20E_%7Bi_p%7D)P(F_%7Bi_1%7D%5Ccap%20%5Ccdots%20%5Ccap%20F_%7Bi_p%7D)%5Cquad%20(X,Y:%20%7B%5Crm%20independent%7D).png)
%3DP(X%3Dkp)/P(E_p)%3DP(X%3Dk).png)
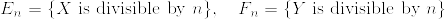
%26%3D%26P%5Cbigg(E_n%5Ccap%20F_n%5Ccap%20%5Cbigcap_%7Bp:%7B%5Crm%20prime%7D%7D(E_%7Bnp%7D%5Ccap%20F_%7Bnp%7D)%5Ec%20%5Cbigg)%5C%5C%0A%26%3D%26E%5Cbigg[1_%7BE_n%5Ccap%20F_n%7DP%5Cbigg(%5Cbigcap_%7Bp:%7B%5Crm%20prime%7D%7D(E_%7Bnp%7D%5Ccap%20F_%7Bnp%7D)%5Ec%7CE_n,F_n%5Cbigg)%5Cbigg]%5C%5C%0A%26%3D%26E[1_%7BE_n%7D1_%7BF_n%7DP(H%3D1)]%5C%5C%0A%26%3D%26n%5E%7B-2s%7D/%5Czeta(2s).png)
%3D%5Cprod_%7Bp:%7B%5Crm%20prime%7D%7D(p1_%7BE_p%7D1_%7BF_p%7D+%5Cmax%20%5C%7B1_%7BE_p%5Ec%7D,1_%7BF_p%5Ec%7D%5C%7D).png)
%3D1/%5Czeta(2s).png)
.png)
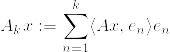
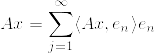

x%7C%5E2%26%3D%26%5Clim_%7BN%5Cto%5Cinfty%7D%5Csum_%7Bn%3Dk+1%7D%5E%7BN%7D%7C%5Clangle%20Ax,e_n%5Crangle%7C%5E2%5C%5C%0A%26%3D%26%5Clim_%7BN%5Cto%5Cinfty%7D%5Csum_%7Bn%3Dk+1%7D%5E%7BN%7D%7C%5Clangle%20x,A%5E*e_n%5Crangle%7C%5E2%5Cquad%20(A%5E*:%20%7B%5Crm%20adjoint~operator%7D)%5C%5C%0A%26%5Cleq%20%26%5Clim_%7BN%5Cto%5Cinfty%7D%7Cx%7C%5E2%5Csum_%7Bn%3Dk+1%7D%5E%7BN%7D%7CA%5E*e_n%7C%5E2%5C%5C%0A%26%3D%26%7Cx%7C%5E2%5Csum_%7Bn%3Dk+1%7D%5E%7B%5Cinfty%7D%7CA%5E*e_n%7C%5E2.png)
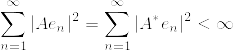
-f(W_0)-%5Cfrac%7B1%7D%7B2%7D%5Cint_0%5Et%5Cbigtriangleup%20f(W_s)ds,%5Cmathcal%7BF%7D_t;%5Cquad%200%5Cleq%20t%3C%5Cinfty.png)
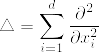
dW_t;%5Cquad%200%5Cleq%20t%5Cleq%20T%5Cquad%20(W:%7B%5Crm%20Brownian%5C%20motion%7D).png)
dt+%5Csigma(t,X_t)dW_t.png)
%3D%5Csum_%7Bj%3D1%7D%5Enc_j(t,x)a_j(t,x),%5Cquad%20%5Cparallel%20b(t,x)%5Cparallel%5E2%3D%5Csum_%7Bj%3D1%7D%5En%7Cc_j(t,x)%7C%5E2.png)
%5E%7B-1%7Db(t,x)%5Cparallel%5E2%5C%5C%0A%26%3D%26b(t,x)%5E%7B%5Ctop%7D(%5Csigma(t,x)%5Csigma(t,x)%5E%7B%5Ctop%7D)%5E%7B-1%7Db(t,x)%5C%5C%0A%26%3D%26%5Csum_%7Bi%3D1%7D%5En%5Csum_%7Bj%3D1%7D%5Enc_i(t,x)c_j(t,x)a_i(t,x)(%5Csigma(t,x)%5Csigma(t,x)%5E%7B%5Ctop%7D)%5E%7B-1%7Da_j(t,x)%5C%5C%0A%26%3D%26%5Csum_%7Bi%3D1%7D%5En%5Csum_%7Bj%3D1%7D%5En%5Cfrac%7Bc_i(t,x)c_j(t,x)%7D%7B%5Clambda_j(t,x)%7Da_i(t,x)a_j(t,x)%5C%5C%0A%26%3D%26%5Csum_%7Bi%3D1%7D%5En%5Cfrac%7Bc_i(t,x)%5E2%7D%7B%5Clambda_i(t,x)%7D%5Cquad%20(%5C%7Ba_i(t,x)%5C%7D:%7B%5Crm%20orthonormal%5C%20basis%7D)%5C%5C%0A%26%5Cleq%20%26%5Cfrac%7B1%7D%7B%5Clambda%7D%5Cparallel%20b(t,x)%5Cparallel%5E2%5C%5C%0A%26%5Cleq%20%26M%5Cquad%20(M:%7B%5Crm%20const%7D,%5Cquad%20b(t,x):%7B%5Crm%20uniformly%5C%20bounded%7D).png)
,(%5COmega,%5Cmathcal%7BF%7D,P),%5C%7B%5Cmathcal%7BF%7D_t%5C%7D.png)
%5E%7B-1%7Db(s,X_s)%5Cparallel%5E2ds%5Cbigg)%5Cbigg]%26%5Cleq%26%5Cexp(Mt/2)%5C%5C%0A%26%3C%26%5Cinfty%20%5Cquad%20(0%5Cleq%20t%3C%5Cinfty).png)
%5E%7B-1%7Db(s,X_s)ds%5Cquad%20(0%5Cleq%20t%5Cleq%20T).png)
dW_s%3D%5Cint_0%5Etb(s,X_s)ds+%5Cint_0%5Et%5Csigma(s,X_s)d%5Ctilde%7BW%7D_s.png)
,(%5COmega,%5Cmathcal%7BF%7D_T,%5Ctilde%7BP%7D_T),%5C%7B%5Cmathcal%7BF%7D_t%5C%7D.png)