Exercise5.2.27
Exercise5.2.27
次の1次元確率微分方程式の解を陽に求めよ.
ただし,Wは1次元ブラウン運動とする.
[解]
%3D%5Csigma(x)%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Csqrt%7B1+x%5E2%7D.png) とすると,この確率微分方程式は
とすると,この確率微分方程式は
の解となる.σ(x)は2階連続微分可能で1階微分,2階微分ともにR上で有界である.b(x)も同様であるから,特にLipschitz連続である.従ってKaratzasShreve Proposition5.2.21より,次の常微分方程式を解くことで上の確率微分方程式の解を得ることができる.
ただし,
これを解いて
以上より解は
となる.[終]
ある種の確率微分方程式が常微分方程式を解くことで解を得ることができるという話題でした.上の場合f(x,y)がxによらないので楽でした.これがxによると常微分方程式を陽に解くことができないので,解析解は出ないように思います.
局所コンパクトハウスドルフ空間上では,ある連続関数の列でG-δコンパクト集合の定義関数に各点収束するものが存在する.
主張
局所コンパクトハウスドルフ(以下LCHとする)X上では,ある連続関数の列でG-δコンパクト集合Kの定義関数に各点収束するものが存在する.
[証明]
次の事実を用いる.
事実
LCHのコンパクト集合Kと開集合OでK⊂Oならば,コンパクト台をもつ実数値連続関数で 0≦u(x)≦1,u(x)=1 (x∈K),supp(u)⊂O となるものが存在する. (猪狩「実解析入門」6章などを参照)
.png) とする.上の事実から各nに対してコンパクト台をもつ連続関数の列
とする.上の事実から各nに対してコンパクト台をもつ連続関数の列 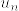 で
で
となるものが存在する.このとき
となる.実際任意のnで 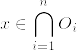 とすると,
とすると, 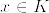 となり矛盾.このnにたいして,
となり矛盾.このnにたいして,%3D0.png)
さらにXが第二可算公理を満たすとコンパクトG_δ集合を含む最小のσ加法族はボレル集合族に一致します.
Exercise5.2.17(Ito-Watanabe(1978))
Problem3.3.23
Problem3.3.23
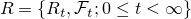 をd(≧3)次元のr(>0)を出発するベッセル過程とする.
をd(≧3)次元のr(>0)を出発するベッセル過程とする. 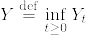 とするとき,
とするとき,
となることを示せ.つまりYはベータ分布に従う.
[証明]
伊藤の公式より,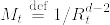 は局所連続マルチンゲールである.従ってあるstopping timeの列
は局所連続マルチンゲールである.従ってあるstopping timeの列 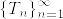 で
で %7D%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7DM_%7BT_n%5Cwedge%20t%7D.png) がマルチンゲールとなり,
がマルチンゲールとなり,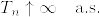 となるものが存在する.
となるものが存在する. %7D%5Cgeq%201/x%5E%7Bd-2%7D%5C%7D.png) ,
, 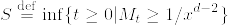 とすると,これらはstopping timeで,
とすると,これらはstopping timeで,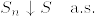 となる.
となる.
で, %7D1_%7B%5C%7BS_n%3D%5Cinfty%5C%7D%7D%7C%5Cleq%201/x%5E%7Bd-2%7D.png) ,
, %7D1_%7B%5C%7B0%3CS_n%3C%5Cinfty%5C%7D%7D%7C%3C1/x%5E%7Bd-2%7D.png) より条件付き期待値のルベーグの収束定理より,
より条件付き期待値のルベーグの収束定理より,
整理して
を得る.[証明終]
Exercise(3.12),Chapter2(Revuz, Yor)続き
つまり
つまり
となる.
(4) )%5Cquad%20(%5Cmu%20%3E0).png) がマルチンゲールであることはすぐにわかる.
がマルチンゲールであることはすぐにわかる. 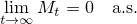 であることを示す.非負のマルチンゲールであるから,
であることを示す.非負のマルチンゲールであるから, 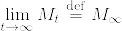 が存在する.Fatouの補題から
が存在する.Fatouの補題から
となり 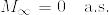 である.よって(1)より
である.よって(1)より %5Cgeq%20x)%3DP(M%5E*%5Cgeq%20%5Cexp(2%5Cmu%20x))%3D%5Cexp(-2%5Cmu%20x).png) となり,結論を得る.[証明終]
となり,結論を得る.[証明終]
Revuz and YorのContinuous Martingales and Brownian Motionという本の問題でした.この問題を使って3次元以上のベッセル過程で0が非再帰的であることが示せるそうなので考えています.今後もこの本の問題を解くかわかりませんが,この本の問題のカテゴリはRevuzAndYorにしておきます.
Exercise(3.12),Chapter2(Revuz, Yor)
Exercise(3.12),Chapter2(Revuz, Yor)
Mを正の値を取る連続マルチンゲールとし,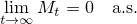 とする.また
とする.また 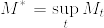 とおく.
とおく.
(1) 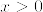 に対して
に対して .png) となることを示せ.
となることを示せ.
(2) より一般に 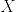 が 正の値を取る
が 正の値を取る 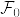 可測な確率変数であるとき
可測な確率変数であるとき .png) であることを示せ.
であることを示せ.
(3) B を .png) を出発する1次元のブラウン運動であるとする.
を出発する1次元のブラウン運動であるとする.  とするとき,
とするとき,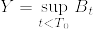 の分布を求めよ.
の分布を求めよ.
(4) B を標準ブラウン運動であるとする. )%5Cquad%20(%5Cmu%20%3E0).png) を用いて
を用いて .png) がパラメータ
がパラメータ 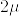 の指数分布に従うことを示せ.
の指数分布に従うことを示せ.
[証明]
(1)  とすると,これはstopping timeでありMはマルチンゲールであるから,
とすると,これはstopping timeでありMはマルチンゲールであるから, もマルチンゲールである.よって
もマルチンゲールである.よって 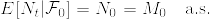 となる.ここで
となる.ここで
%7C%3C%20x%20%5Cquad%20%5Cforall%7Bt%7D.png) ,
,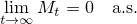 であるから条件付き期待値のルベーグの収束定理より
であるから条件付き期待値のルベーグの収束定理より
となる.一方
となり,
となる.2つ目の等式は  であることと条件付き期待値のルベーグの収束定理から従う.以上より
であることと条件付き期待値のルベーグの収束定理から従う.以上より
よって
[(1)の証明終][次の記事に続きます]
dt%20+%20%5Csqrt%7B1+X_t%5E2%7D%5C%20dW_t,%5Cquad%20P(X_0%3D%5Cxi)%3D1.png)
+%5Cfrac%7B1%7D%7B2%7D%5Csigma(X_s)%5Csigma'(X_s)%5Cbigg%5C%7Dds+%5Cint_0%5Et%5Csigma(X_s)dW_s.png)
,%5Cquad%20u(0,y)%3Dy..png)
%3Df(W_t(%5Comega),Y_t(%5Comega))%5Cquad%20%7B%5Crm%20with%7D%5Cquad%20Y_0(%5Comega)%3D%5Cxi(%5Comega).png)
%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Cfrac%7B1%7D%7B%5Crho%20(x,y)%7D,%5Cquad%20f(x,y)%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7D%5Crho(x,y)b(u(x,y))..png)
%3D%5Cfrac%7B1%7D%7B2%7D%5Cbigg%5C%7B(%5Csqrt%7B1+y%5E2%7D+y)e%5Ex-(%5Csqrt%7B1+y%5E2%7D-y)e%5E%7B-x%7D%5Cbigg%5C%7D.png)
%3D%5Csqrt%7B1+y%5E2%7D.png)
%3D%5Cfrac%7B1%7D%7B2%7D%5Cbigg%5C%7B(%5Csqrt%7B1+%5Cxi%5E2(%5Comega)%7D+%5Cxi(%5Comega))e%5Et-(%5Csqrt%7B1+%5Cxi%5E2(%5Comega)%7D-%5Cxi(%5Comega))e%5E%7B-t%7D%20%5Cbigg%5C%7D.png)
%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B2%7D%5Cbigg%5C%7B(%5Csqrt%7B1+Y_t%5E2%7D+Y_t)e%5E%7BW_t%7D-(%5Csqrt%7B1+Y_t%5E2%7D-Y_t)e%5E%7B-W_t%7D%20%5Cbigg%5C%7D%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7B2%7D%5Cbigg%5C%7B(%5Csqrt%7B1+%5Cxi%5E2%7D+%5Cxi)e%5E%7Bt+W_t%7D%20-(%5Csqrt%7B1+%5Cxi%5E2%7D-%5Cxi)e%5E%7B-t-W_t%7D%5Cbigg%5C%7D.png)
%5Csubset%20%5Cbigcap_%7Bi%3D1%7D%5EnO_i,%5Cquad%20u_n(x)%3D1%5Cquad%20(x%5Cin%20K).png)
%3D%5Cleft%5C%7B%0A%5Cbegin%7Barray%7D%7Bll%7D%0A1%5Cquad%20(x%5Cin%20K)%5C%5C%0A0%5Cquad%20(x%5Cnot%5Cin%20K)%0A%5Cend%7Barray%7D%0A%5Cright..png)
%3D1%5Cquad%20(x%5Cin%20K).png)
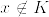
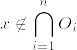
%3D0%5Cquad(x%5Cnot%20%5Cin%20K).png)
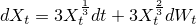
%7D%3D%5Cleft%5C%7B%0A%5Cbegin%7Barray%7D%7Bll%7D%0A0;%5Cquad%20%260%5Cleq%20t%3C%5Cbeta_%7B%5Ctheta%7D%5C%5C%0AW_t%5E3;%5Cquad%20%26%5Cbeta_%7B%5Ctheta%7D%5Cleq%20t%3C%5Cinfty%0A%5Cend%7Barray%7D%0A%5Cright..png)
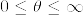
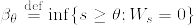
%7D.png)
%7D%3D0)%3D1.png)
%5E2%20%5C%7Dds%5Cbigg]%3D%5Cint_0%5EtE%5C%7B%20%7C3X_s%5E%7B%5Cfrac%7B1%7D%7B3%7D%7D%7C+(3X_s%5E%7B%5Cfrac%7B2%7D%7B3%7D%7D)%5E2%20%5C%7Dds%3C%5Cinfty%5Cquad%20(%5Cforall%7Bt%7D%5Cgeq%200,%20%7B%5Crm%20Fubini%7D).png)
%5E2%20%5C%7Dds%3C%5Cinfty%5Cbigg]%3D1.png)
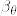
%7D%3D(W_t-W_%7Bt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D%7D)%5E3.png)
%7D%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7DW_t-W_%7Bt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D%7D.png)
%7D%3D(Z_t%5E%7B(%5Ctheta)%7D)%5E3%3D3%5Cint_0%5EtZ_s%5E%7B(%5Ctheta)%7Dd%5Clangle%20Z%5E%7B(%5Ctheta)%7D%5Crangle%20_s+3%5Cint_0%5Et(Z_s%5E%7B(%5Ctheta)%7D)%5E2dZ%5E%7B(%5Ctheta)%7D_s.png)
%7D_t%3D%5Cleft%5C%7B%0A%5Cbegin%7Barray%7D%7Bll%7D%0A0;%5Cquad%20%26(0%5Cleq%20t%3C%5Cbeta_%7B%5Ctheta%7D)%5C%5C%0AW_t;%5Cquad%20%26(%5Cbeta_%7B%5Ctheta%7D%5Cleq%20t%3C%5Cinfty)%0A%5Cend%7Barray%7D%0A%5Cright..png)
%7D%3D3%5Cint_0%5EtX_s%5E%7B(%5Ctheta)%7Dds+3%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E2dW_s.png)
%7D%5Cstackrel%7B%7B%5Crm%20def%7D%7D%7B%3D%7DW_%7Bt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D%7D.png)
%7D)%5E%7B2/3%7DdZ_s%5E%7B(%5Ctheta)%7D%3D%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B2/3%7DdW_s-%5Cint_0%5Et%20(X_s%5E%7B(%5Ctheta)%7D)%5E%7B2/3%7DdA_s%5E%7B(%5Ctheta)%7D.png)
%7D)%5E%7B2/3%7DdA_s%5E%7B(%5Ctheta)%7D%5Cbigg)%5E2%5C%20%5Cbigg]%3DE%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B4/3%7Dd%5Clangle%20A%5E%7B(%5Ctheta)%7D%5Crangle_s.png)
%7D%5Crangle_t%3Dt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D.png)
%7D)%5E%7B4/3%7Dd%5Clangle%20A%5Crangle_s%5E%7B(%5Ctheta)%7D%5C%5C%0A%26%3D%26%5Cint_0%5E%7Bt%5Cwedge%20%5Cbeta_%7B%5Ctheta%7D%7D(X_s%5E%7B(%5Ctheta)%7D)%5E%7B4/3%7Dd%5Clangle%20A%5Crangle_s%5E%7B(%5Ctheta)%7D%3D0%5Cquad%20(X_t%5E%7B(%5Ctheta)%7D%3D0%5Cquad%200%5Cleq%20%5Cforall%7Bt%7D%5Cleq%20%5Cbeta_%7B%5Ctheta%7D).png)
%7D)%5E%7B1/3%7Dd%5Clangle%20Z%5E%7B(%5Ctheta)%7D_s%5C%5C%0A%26%3D%26%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B1/3%7Dds-2%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B1/3%7Dd%5Clangle%20W,A%5E%7B(%5Ctheta)%7D%5Crangle%20_s+%5Cint_0%5Et(X_s%5E%7B(%5Ctheta)%7D)%5E%7B1/3%7Dd%5Clangle%20A%5E%7B(%5Ctheta)%7D%5Crangle_s.png)
%7D)%5E%7B1/3%7Dd%5Clangle%20A%5E%7B(%5Ctheta)%7D%5Crangle_s%3D0.png)
%7D)%5E%7B1/3%7Dd%5Clangle%20W,A%5E%7B(%5Ctheta)%7D%5Crangle%20_s%5Cbigg%7C%5Cleq%20%5Cbigg(%5Cint_0%5Et%20(X_s%5E%7B(%5Ctheta)%7D)%5E%7B2/3%7Dd%5Clangle%20A%5E%7B(%5Ctheta)%7D%5Crangle_s%5Cbigg)%5E%7B1/2%7D%5Cbigg(%5Cint_0%5Et1ds%5Cbigg)%5E%7B1/2%7D%3D0.png)
%3D%5Cbigg(%5Cfrac%7Bx%7D%7Br%7D%5Cbigg)%5E%7Bd-2%7D%5Cquad%20(0%5Cleq%20x%5Cleq%20r).png)
%7D%7C%5Cmathcal%7BF%7D_0]%3DM_%7B0%5Cwedge%20S_n%7D%5E%7B(n)%7D%3D1/r%5E%7Bd-2%7D%5Cquad%20%7B%5Crm%20a.s.%7D.png)
%7D%3DM_t%5E%7B(n)%7D1_%7B%5C%7BS_n%3D%5Cinfty%5C%7D%7D+M_%7Bt%5Cwedge%20S_n%7D%5E%7B(n)%7D1_%7B%5C%7B0%3CS_n%3C%5Cinfty%5C%7D%7D+M_0%5E%7B(n)%7D1_%7B%5C%7BS_n%3D0%5C%7D%7D.png)
%7D1_%7B%5C%7BS_n%3D%5Cinfty%5C%7D%7D%7C%5Cmathcal%7BF%7D_0]%3DE[M_%7BT_n%7D1_%7B%5C%7BS_n%3D%5Cinfty%5C%7D%7D%7C%5Cmathcal%7BF%7D_0].png)
%7D1_%7B%5C%7B0%3CS_n%3C%5Cinfty%5C%7D%7D%7C%5Cmathcal%7BF%7D_0]%3DE[M_%7BS_n%7D%5E%7B(n)%7D1_%7B%5C%7B0%3CS_n%3C%5Cinfty%5C%7D%7D%7C%5Cmathcal%7BF%7D_0].png)
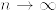
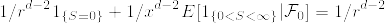
%3D1%5Cwedge%20(x/r)%5E%7Bd-2%7D.png)
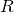
%3D1.png)
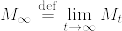
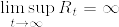
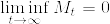
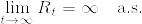
%5C%7D%7D.png)
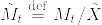
%3D1%5Cwedge%20%5Ctilde%7BM%7D_0.png)
%5C%7D%7D%7C%5Cmathcal%7BF%7D_0)%3D1%5Cwedge%20M_0/(X1_%7B%5C%7BX%5Cin(1/n,n)%5C%7D%7D).png)
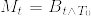
%3D1.png)
%3D1%5Cwedge%20a/x.png)
%3D1%5Cwedge%20a/x.png)
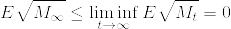
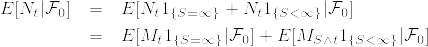


.png)
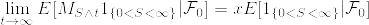

1_%7B%5C%7BS%3D0%5C%7D%7D+xP(M%5E*%5Cgeq%20x%7C%5Cmathcal%7BF%7D_0)%3DM_0.png)
%5Cgeq%20x.png)
%3D0.png)
+xP(M%5E*%5Cgeq%20x%7C%5Cmathcal%7BF%7D_0)%3DM_0.png)
%3D1.png)
%3DM_0.png)
%3DM_0/x.png)
%3D1%5Cwedge%20(M_0/x).png)